Signe d'une fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 25 Nov 2015, 13:44
par adamNIDO » 25 Nov 2015, 13:44
Bonjour

Merci d'avance
on a

On a

est une fonction dérivable sur
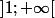
comme somme de deux fonction usuelle dérivable sur
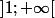
donc
=\dfrac{x}{\sqrt{x^2-1}}-1=\dfrac{x-\sqrt{x^2-1}}{\sqrt{x^2-1}})
son signe est celui de :
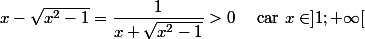
Donc

f est strictement croissante sur

je suis bloque dans la question de signe j'ai calcule
=-4<0)
et
=-3)
Merci d'avance

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 26 Nov 2015, 00:30
par Lostounet » 26 Nov 2015, 00:30
Je ne trouve pas d'erreur... La fonction g est bien continue sur [1; + oo[ comme somme de fonctions usuelles continues.
Et l'image d'un intervalle par une fonction continue est un intervalle, et celui-ci est inclus dans R-.
C'est valable comme justification?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Anonyme
 par Anonyme » 26 Nov 2015, 08:50
par Anonyme » 26 Nov 2015, 08:50
adamNIDO a écrit:Bonjour

Merci d'avance
on a

On a

est une fonction dérivable sur
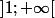
comme somme de deux fonction usuelle dérivable sur
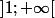
donc
=\dfrac{x}{\sqrt{x^2-1}}-1=\dfrac{x-\sqrt{x^2-1}}{\sqrt{x^2-1}})
son signe est celui de :
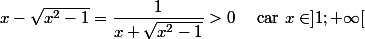
Donc

f est strictement croissante sur

je suis bloque dans la question de signe j'ai calcule
=-4<0)
et
=-3)
Merci d'avance
Bonjour,
Selon ce que tu parviens à faire, deux possibilités:
1. résoudre g(x)=0(possible)
2. tu ne parviens pas à résoudre g(x)=0 et tu justifies l'unicité de la solution avec le théorème de la valeur intermédiaire en en donnant ensuite une valeur approchée avec la calculatrice.
et ensuite utiliser les variations de g et sa continuité
A savoir, si g(

)=0 on a g(x)<0 sur [1;

[...

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 26 Nov 2015, 10:53
par Lostounet » 26 Nov 2015, 10:53
maths-lycee fr a écrit:Bonjour,
Selon ce que tu parviens à faire, deux possibilités:
1. résoudre g(x)=0(possible)
2. tu ne parviens pas à résoudre g(x)=0 et tu justifies l'unicité de la solution avec le théorème de la valeur intermédiaire en en donnant ensuite une valeur approchée avec la calculatrice.
et ensuite utiliser les variations de g et sa continuité
A savoir, si g(

)=0 on a g(x)<0 sur [1;

[...
On applique simplement le théorème de la bijection entre l'intervalle et son image vu la monotonie de g (continue).
Pourquoi résoudre g(x)=0?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 26 Nov 2015, 10:58
par adamNIDO » 26 Nov 2015, 10:58
Merci beaucoup mais si j'ai raisonne comme cela :
On a
=\dfrac{x}{\sqrt{x^{2}-1} }-1)
, toujours positive sur l' intervalle
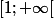
, donc

est croissante strictement (

est nulle en un seul nombre) sur le même intervalle, vu qu'elle est continue , on a donc
 =[g(1) ;\lim_{x\to +\infty}g(x)[=[-4;-3[)
Et donc

est négative sur l intervalle
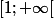

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 26 Nov 2015, 11:03
par Lostounet » 26 Nov 2015, 11:03
En quel point g' s'annule?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
mathelot
 par mathelot » 26 Nov 2015, 11:12
par mathelot » 26 Nov 2015, 11:12
ave la quantité conjuguée on obtient:
=- \frac{6x+10}{\sqrt{x^2-1}+x+3})
donc négative sur D(f) (ensemble de définition)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 26 Nov 2015, 11:14
par adamNIDO » 26 Nov 2015, 11:14
Lostounet a écrit:En quel point g' s'annule?
oui il s'annule pas


-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 26 Nov 2015, 11:21
par Lostounet » 26 Nov 2015, 11:21
Le -1 n'est pas dans le dénominateur...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Anonyme
 par Anonyme » 26 Nov 2015, 11:24
par Anonyme » 26 Nov 2015, 11:24
Lostounet a écrit:En quel point g' s'annule?
Nulle part mais s'il a compris son cours, il doit pouvoir s'en apercevoir...
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 26 Nov 2015, 11:24
par adamNIDO » 26 Nov 2015, 11:24
mathelot a écrit:ave la quantité conjuguée on obtient:
=- \frac{6x+10}{\sqrt{x^2-1}+x+3})
donc négative sur D(f) (ensemble de définition)
Bonjour,
la question 1 on a trouvé les variation de g a savoir que g est strictement croissante sur
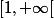
comment daprès cette question déduire le signe de g
mais ce que tu as fait je pense que c'est une autre façon de trouve le sign de g
Pour tout

dans
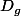
:
=- \frac{6x+10}{\sqrt{x^2-1}+x+3}<0)
Merci d'avance

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 26 Nov 2015, 11:26
par Lostounet » 26 Nov 2015, 11:26
maths-lycee fr a écrit:Nulle part mais s'il a compris son cours, il doit pouvoir s'en apercevoir...
Oui moi je sais, je voulais qu'il me le dise :marteau:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 26 Nov 2015, 11:30
par adamNIDO » 26 Nov 2015, 11:30
Lostounet a écrit:Oui moi je sais, je voulais qu'il me le dise :marteau:
si j'ai bien compris
on a pour tout

dans
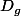
\leq -3)
et que g' ne s'annule pas et continue donc n'admet pas de maximum ou de minimum donc g forcement négative
c'est ca n'est pas
Merci d'avance

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 26 Nov 2015, 11:35
par Lostounet » 26 Nov 2015, 11:35
Tu as dit dans ton post "g' s'annule une seule fois". Lequel?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 26 Nov 2015, 11:39
par adamNIDO » 26 Nov 2015, 11:39
Lostounet a écrit:Tu as dit dans ton post "g' s'annule une seule fois". Lequel?
salut,
non j'ai rectifie il ne s'annule pas j'ai poste une photo de mathematica qui preuve que g' ne s'annule pas
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 26 Nov 2015, 14:09
par adamNIDO » 26 Nov 2015, 14:09
Bonjour,
ce que j'ai fait est correct
Merci d'avance
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 28 Nov 2015, 10:23
par adamNIDO » 28 Nov 2015, 10:23
Bonjour,
est ce que mon preuve est correcte de plus est ce que c'est suffisante au niveau Lycée de dire que g est strictement croissante et que son limite a l'infinie est
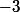
donc pour tout

dans
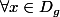
\leq -3)
Merci d'avance
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 28 Nov 2015, 19:25
par adamNIDO » 28 Nov 2015, 19:25
Bonsoir
est ce que mon preuve est correcte de plus est ce que c'est suffisante au niveau Lycée de dire que g est strictement croissante et que son limite a l'infinie est
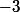
donc pour tout

dans
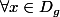
\leq -3)
Merci d'avance
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 29 Nov 2015, 10:53
par adamNIDO » 29 Nov 2015, 10:53
Bonjour,
votre aide s'il vous plait
Merci d'avance
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 29 Nov 2015, 15:13
par adamNIDO » 29 Nov 2015, 15:13
Bonjour,
est ce que mon raisonnement est correct
Merci d'avance
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités



est une fonction dérivable sur
comme somme de deux fonction usuelle dérivable sur
son signe est celui de :
f est strictement croissante sur
et
)=0 on a g(x)<0 sur [1;
[...