Sens de variation

[acdc-27]

bonjour a tous , j'aurais aimé savoir :

avec
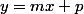
et (D) d'équation et A(1;-1)
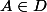
si et seulement si -1= m +p

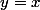
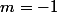
=> D a pour équation car on trouve et

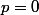
1) etudier les variation de f

ce que j'ai fais : f(x) est possible , à condition que ait nous allons étudier les variations de f , afin d'observer son sens de variation .






j'arrive à ça , mais je suis pas sûr du résultat pour continuer le tableau de variation ...

[flo22]

Bonsoir,

qu'est ce que D ? Une droite passant par A mais après ?

Mais ta dérivée semble bonne.

[acdc-27]

bah c'étais juste ça l'énoncer ... je me suis pas préoccupé de D en faite . . . aurais-je du ?

comment dresser le tableau de variation avec ma dérivée je vois pas . . .

(PS: je passe en 1ere S )

[flo22]

Comment connais-tu les dérivées ? On voit pas ça en seconde si ? Tu connais le lien dérivée-sens de variation ?

[acdc-27]

oui c'est vrai , sa parait confu comme sa , mais j'étudie mes chapitre en vacance :) en gros je m'avance par mes propres moyens :)

[flo22]

OK, donc tu dois aimer les maths, puis si tu vas en 1ère S vaudrait mieux un petit peu mieux rédiger, je t'expliquerai plus tard.

Mais pour l'instant, connais-tu le lien sens de variation d'une fonction f / dérivée de cette fonction ?

[acdc-27]

non pas tellement , mais je veux bien des explications :)

oui , ma rédaction est un peu confuse là :s

[flo22]

Tu verra l'année prochaine que pour connaitre les variations d'une fonction (tu vois bien de quoi je parle là ?), il faut étudier le signe de la dérivée.

Plus précisément : f est croissante si et seulement si f'>0
f est décroissante si et seulement si f'<0

Je te passe les problèmes qu'il peut y avoir, tu les verra bien assez tôt (notamment, on ne peut pas dériver toutes les fonctions en chaque point)

[acdc-27]

ouais ça j'ai compris :)
pourquoi tu as des problèmes à me refiler ? :D
mais parcontre pour mon tableau de variation je vois pas , parce que :

-oo -1 1-2x +oo

franchement sur ça je veux bien une explication , je suis perdu arrivé ici ...

[flo22]

Il faut étudier le signe de , c'est à dire déterminer pour quel(s) x de l'ensemble de définition de f cette expression est positive ou négative. Normalement on fait ça en seconde, quand on résout des inéquations. Tu ne vois pas ?

[acdc-27]

c'est pas qu'en on fais : ?? un truc de se genre ?

[flo22]

Par exemple, si je te demande de résoudre tu t'y prends comment ?

[acdc-27]

L'ensemble D de définition de l'inéquation est : (3x-1)/(x+1)
d'ou : x + 1;)0 donc D = ]-oo;-1[U]-1;+oo[

donc S = ]-1;1/3]

[flo22]

Ton ensemble de solution est bon, mais je comprends pas trop comment tu as fait. Tu as fait un tableau avec les signes du dénominateur et du numérateur puis tu as appliquer les règles " +*+=+, -*+=- etc" ?
Par ailleurs, tu dis

L'ensemble D de définition de l'inéquation est : (3x-1)/(x+1) <ou= 0

ça ne veut rien dire : l'ensemble de définition d'une expression, c'est l'ensemble des valeurs que peut prendre x. ( c'est bien ce que tu as fait après, mais tu aurai dû dire " l'ensemble de déf.... est D = ]-oo;-1[U]-1;+oo[

[acdc-27]

bah en sachant que dans ce cas de figure , le dénominateur doit etre ;) 0 sinon . . . impossible donc x +1 ;) 0 soit x;) -1

et 3x-1 => -b/a => 1/3

et j'ai oublier : je cite "L'ensemble D de définition de l'inéquation (F) : ...."

[flo22]

Oui je suis d'accord, mais tu t'es mal exprimer ^^
Sinon, tu as fait comme j'ai dit, avec un tableau ?

[acdc-27]

a vrai dire pour cette inéquation non , mais en faisant le tableau :

X -oo -1 1/3 +oo

3x-1 - - 0 +


x+1 - 0 + +


f(x) + || - 0 +

[acdc-27]

pas trés bien fais mon tableau . . . :(

[flo22]

C'est bien ce dont je parlais. Bref, revenons à nos moutons : tu peux faire la même chose pour ta dérivée : sauf qu'ici c'est encore plus simple ! Réfléchis un petit peu ;)

[acdc-27]

ouais mais la dérivée d'un quotient c'est u'v-uv' / v² . . . . ??