Ecrire, lorsque c'est possible, f(x) sous la forme d'un produit de facteurs du premier degré dans chacun des cas suivants :
1) f(x) = 3x² + 16x -35
2) f(x) = 3x² + 16x +35
3) f(x) = 28.8 + 5x² - 24x
4) f(x) = 42 - 29x - 5x²
:id:
Second degré
10 messages
- Page 1 sur 1
C'est simple.
Je te montre pour le 1er. Tu dois trouver a, b et c.
a = x²
b = x
c = 1 (n'importe quel chiffre)
Une fois trouvé, tu dois utiliser Delta (;))
Formule de (delta) :
(delta) :
 = b²- 4ac
= b²- 4ac
Si >0 Il y aura 2 solutions :
>0 Il y aura 2 solutions :

Donc S = {x : x}
x = nombre de la solution
Si =0 Il y aura une solution
=0 Il y aura une solution

Donc S = {x}
Si <0
<0
S = ø
Pour le 1er :
f(x) = 3x² + 16x -35
a = 3
b = 16
c = - 35
Il faut utiliser (delta)
(delta)
 = (16)² - 4*3*(-35)
= (16)² - 4*3*(-35)
 = 256 + 420
= 256 + 420
 = 676
= 676
 = 26 (Il faut utiliser Racine de + le nombre)
= 26 (Il faut utiliser Racine de + le nombre)
x1 = - 16 + 26/2*3
x1 = 10/6
(tu peut laisser comme ça, ou réduire à 1,66)
x2 = - 16 - 26/6
x2 = -42/6
x2 = 7
S= {10/6 ; 7}
Voilà voilà
Je te montre pour le 1er. Tu dois trouver a, b et c.
a = x²
b = x
c = 1 (n'importe quel chiffre)
Une fois trouvé, tu dois utiliser Delta (;))
Formule de
Si

Donc S = {x : x}
x = nombre de la solution
Si

Donc S = {x}
Si
S = ø
Pour le 1er :
f(x) = 3x² + 16x -35
a = 3
b = 16
c = - 35
Il faut utiliser
x1 = - 16 + 26/2*3
x1 = 10/6
(tu peut laisser comme ça, ou réduire à 1,66)
x2 = - 16 - 26/6
x2 = -42/6
x2 = 7
S= {10/6 ; 7}
Voilà voilà
un petit rappel s'impose alors
un polynome du second degré est une expression de la forme ax²+bx+c (a,b,c réels , avec a#0) pour trouver les eventuelles racines du polynôme on pose .
.
1) si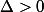 le polynôme admet 2 racines distinctes :
le polynôme admet 2 racines distinctes :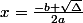 ou
ou 
2) si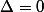 le polynôme a une racine double
le polynôme a une racine double
3) si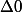 donc f(x) admet 2 racines distinctes :
donc f(x) admet 2 racines distinctes :

 ou
ou 
 ou
ou 
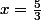 ou
ou 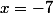
donc(x+7))
essaie de faire les autres
un polynome du second degré est une expression de la forme ax²+bx+c (a,b,c réels , avec a#0) pour trouver les eventuelles racines du polynôme on pose
1) si
2) si
3) si
donc
essaie de faire les autres
Onizuka a écrit:C'est simple.
Je te montre pour le 1er. Tu dois trouver a, b et c.
a = x²
b = x
c = 1 (n'importe quel chiffre)
Une fois trouvé, tu dois utiliser Delta (;))
Formule de(delta) :
= b²- 4ac
Si>0 Il y aura 2 solutions :
Pour le 1er :
f(x) = 3x² + 16x -35
a = 3x²
b = 16 x
c = - 35
Il faut utiliser(delta)
= (16x)² - 4x²*(-35=
=
C'est faux, et ARCHIFAUX
Si on a ax²+bx+c= 0
Alors
Donc pour f(x) = 3x² + 16x -35
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
