Second degré...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 12 Juin 2006, 18:48
par axiome » 12 Juin 2006, 18:48
Bonjour, je voudrais savoir si, pour un trinôme du second degré ax²+bx+c, il existe une condition suffisante pour que ce trinôme admette deux racines.
merci d'avance à ceux qui voudront bien me répondre.
La vie nest bonne quà étudier et à enseigner les mathématiques.
Blaise PASCAL
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Juin 2006, 19:04
par Nightmare » 12 Juin 2006, 19:04
Bonsoir
Il faut et il suffit que b²-4ac soit strictement positif
:happy3:
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 12 Juin 2006, 19:09
par axiome » 12 Juin 2006, 19:09
ceci nightmare est une condition nécessaire et suffisante. Moi je voudrais une condition suffisante seulement. je crois que ça existe mais je ne me rappelle plus du tout ce que c'est.
-
titoui
- Messages: 3
- Enregistré le: 10 Juin 2006, 18:48
-
 par titoui » 12 Juin 2006, 20:46
par titoui » 12 Juin 2006, 20:46
il en existe plein comme par exemple b=0 et

strictement positif mais ça n'a pas un grand interet.
-
corder299
- Messages: 5
- Enregistré le: 12 Juin 2006, 15:40
-
 par corder299 » 12 Juin 2006, 22:16
par corder299 » 12 Juin 2006, 22:16
Euh je me trompe peut être mais si delta est negatif l'expression admet aussi deux racines complexe non ?
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 13 Juin 2006, 13:48
par allomomo » 13 Juin 2006, 13:48
Salut,
un polynome de degré n admet n solutions dans C.
Théorème d'un philosophe : D'Alambert je pense
-
murray
- Membre Naturel
- Messages: 84
- Enregistré le: 17 Mai 2006, 17:50
-
 par murray » 13 Juin 2006, 13:57
par murray » 13 Juin 2006, 13:57
bonjour,
c'est le théorème de Gauss-d'Alembert allomomo: tout polynôme est scindé
dans C[X]
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 14 Juin 2006, 22:16
par axiome » 14 Juin 2006, 22:16
ouf ça y est j'ai retrouvé la feuille avec la réponse à mon problème...
En fait, il suffit simplement que a et c soient de signe contraire.
Merci à tous ceux qui ont bien voulu me répondre.
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 14 Juin 2006, 22:41
par BancH » 14 Juin 2006, 22:41
C'était évident:
Avec

:
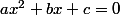
^2 - (\frac{bx}{2x\sqrt a})^2+c=0)
^2 - (\frac{b}{2\sqrt a})^2+c=0)
^2 = (\frac{b}{2\sqrt a})^2-c)

ce polynôme admet deux racines si

Pour avoir

il suffit d'avoir

et

Avec
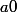
Pour avoir

il suffit d'avoir
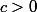
car

et

-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 15 Juin 2006, 06:03
par nox » 15 Juin 2006, 06:03
sympa comme démo...mais bon perso j'aurai juste dit que pour que
b² - 4ac > 0
b² > 4ac
ce qui est sur si a et c sont de signes contraires ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
