j'ai besoin d'aide pour cet exercice
soit a, b et c positives montrerque sqrt(2a/(a+b))+sqrt(2b/(c+b))+sqrt(2c/(a+c))<3
Salut!
11 messages
- Page 1 sur 1
Salut,
Si on pose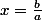 ;
;  et
et  donc avec
donc avec  et
et 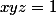 ton énoncé revient à montrer que
ton énoncé revient à montrer que 
Or, pour un produit fixé, si on étudie (pour
fixé, si on étudie (pour  )
)  = \frac{1}{\sqrt{1+x}}+\frac{1}{\sqrt{1+y}} = (1+x)^{-\frac{1}{2}} + (1+\frac{a}{x})^{-\frac{1}{2}})
on a =-\frac{1}{2} (1+x)^{-\frac{3}{2}} +\frac{a}{2x^2} (1+\frac{a}{x})^{-\frac{3}{2}})
donc>0\ \Leftrightarrow\ x^4(1+\frac{a}{x})^3 0) et
et 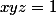 ) lorsque
) lorsque  et celà donne le résultat escompté.
et celà donne le résultat escompté.
P.S. : il doit y avoir plus simple en utilisant les fonctions symétriques élémentaires...
Si on pose
Or, pour un produit
on a
donc
P.S. : il doit y avoir plus simple en utilisant les fonctions symétriques élémentaires...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Je "n'élimine" pas le z : je considère juste, dans un premier temps que c'est une constante fixée et je regarde quel est le maximum de la somme des deux autres termes (pour rendre la plus frand possible une somme de 3 termes dont un des trois est fixé, ben il suffit de maximiser la somme des deux autres...)
De toute façon, ce que j'ai fait, ça déconne sur la fin : je m'était gourré dans les calculs la première fois et quand j'ai rectifié, je me suis retrouvé avec le facteur x²+a(a-3)x+a lors du calcul de f'>0 et ce facteur n'est pas forcément positif (ça dépend si a>4 ou pas).
Ca marche quand même, mais ça rallonge vachement la preuve vu qu'il faut déterminer les racines de x²+a(a-3)x+a et faire pas mal de calculs avec ces racines...
Tout ça pour conclure que je pense qu'il y a nettement plus simple mais bon, j'ai pas trouvé... :hum:
A mon avis, tu devrais mettre ton énoncé dans la rubrique "olympiades" du forum : je ne pense pas que ce soit un truc "usuel" qu'on demande à un lycéen en françe ton inégalité.
De toute façon, ce que j'ai fait, ça déconne sur la fin : je m'était gourré dans les calculs la première fois et quand j'ai rectifié, je me suis retrouvé avec le facteur x²+a(a-3)x+a lors du calcul de f'>0 et ce facteur n'est pas forcément positif (ça dépend si a>4 ou pas).
Ca marche quand même, mais ça rallonge vachement la preuve vu qu'il faut déterminer les racines de x²+a(a-3)x+a et faire pas mal de calculs avec ces racines...
Tout ça pour conclure que je pense qu'il y a nettement plus simple mais bon, j'ai pas trouvé... :hum:
A mon avis, tu devrais mettre ton énoncé dans la rubrique "olympiades" du forum : je ne pense pas que ce soit un truc "usuel" qu'on demande à un lycéen en françe ton inégalité.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
Si on pose;
et
donc avec
et
ton énoncé revient à montrer que
Or, pour un produitfixé, si on étudie (pour
)
 = \frac{1}{\sqrt{1+x}}+\frac{1}{\sqrt{1+y}} = (1+x)^{-\frac{1}{2}} + (1+\frac{a}{x})^{-\frac{1}{2}})
on a
doncet
) lorsque
et celà donne le résultat escompté.
P.S. : il doit y avoir plus simple en utilisant les fonctions symétriques élémentaires...
Ça ne marche pas puisque pour
:zen:
j'avais déjà signalé que c'était faux :
De plus, la borne supérieure de f n'est jamais 1.
Si c'est
c'est >1)
Si c'est
c'est =f(x_2)=(1+x_1)^{-1/2}+(1+x_2)^{-1/2}>1) où
où  et
et  désignent les deux racines de
désignent les deux racines de X+a) (donc
(donc 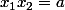 et on est sûr que
et on est sûr que 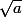 est entre les deux)
est entre les deux)
Ben314 a écrit:...je m'était gourré dans les calculs la première fois et quand j'ai rectifié, je me suis retrouvé avec le facteur x²+a(a-3)x+a lors du calcul de f'>0 et ce facteur n'est pas forcément positif (ça dépend si a>4 ou pas)...
De plus, la borne supérieure de f n'est jamais 1.
Si
Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
