[Défi 1°S] Révisions polynômes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Juil 2010, 20:05
par Dinozzo13 » 21 Juil 2010, 20:05
Bonsoir, je poste ce soir un petit défi à l'attention de ceux et celle qui souhaiterais réviser/approfondir un peu sur les polynômes. Amusez-vous bien.
Soit le polynôme

défini par :
=x^4-4x^3-11x^2+12x+9)
1°)a) Vérifier que
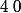
n'est pas racine de ce polynôme.
b) Que peut-on en déduire concerant le réel

?
2°) Montrer que si
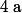
est racine de

alors

est aussi racine de

.
3°) On pose

.
a) Montrer que :
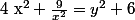
b) Exprimer
}{x^2})
en fonction de
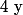
; calculer les racines du trinôme d'inconnue
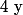
ainsi obtenu.
c) En déduire les solutions de
=0)
.
Une correction détaillée sera disponible en cas de besoin :++:
Bon travail :++:

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Juil 2010, 11:30
par Lostounet » 22 Juil 2010, 11:30
Dinozzo13 a écrit:Soit le polynôme

défini par :
=x^4-4x^3-11x^2+12x+9)
1°)a) Vérifier que
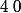
n'est pas racine de ce polynôme.
b) Que peut-on en déduire concerant le réel

?
Salut!
1) a - On remplace x par 0 pour trouver que.. cette valeur n'annule pas le polynôme! - Donc...
b - Que P(0) est non nul?
Pour celle qui suit, je n'arrive pas :triste:
Des pistes?
Merci d'avance

Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 22 Juil 2010, 11:34
par ffpower » 22 Juil 2010, 11:34
Précise un peu l'énoncé du 1-b) parce que c est pas clair du tout. Tu demandes de déduire quelque chose sur un réel x que tu n'as pas défini..
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 22 Juil 2010, 11:52
par Dinozzo13 » 22 Juil 2010, 11:52
Oui en effet, j'ai mal posé la question, excusez-moi :
j'aurai du dire :
1°)b) Quel remarque peut-on faire concernant le réel x s'il est racine de P ? Mais je trouvais que ca guidais trop mais bon.
:++:
@Lostounet : a racine de P implique ?
Calcule
)
et montre donc que
=?)

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Juil 2010, 12:03
par Lostounet » 22 Juil 2010, 12:03
Dinozzo13 a écrit:Oui en effet, j'ai mal posé la question, excusez-moi :
j'aurai du dire :
1°)b) Quel remarque peut-on faire concernant le réel x s'il est racine de P ? Mais je trouvais que ca guidais trop mais bon.
:++:
@Lostounet : a racine de P implique ?
Calcule
)
et montre donc que
=?)
a racine de P implique P(a) = 0.. :briques:
Sinon, je trouve:
 = \frac{81}{a^4} + 4\frac{27}{a^3} - 11\frac{9}{a^2} - 12\frac{3}{a} + 9)
Sauf erreur..
Je joue avec l'écriture jusqu'à ce que je trouve quelque chose? :id:
Faudrait que je trouve que P(a) = P(-a/3)
Et si a racine, donc - a/3 l'est aussi?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Anonyme
 par Anonyme » 22 Juil 2010, 12:09
par Anonyme » 22 Juil 2010, 12:09
Cétait pas

? :zen:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 22 Juil 2010, 12:10
par Dinozzo13 » 22 Juil 2010, 12:10
Met tout au même dénominateur puis montre que le numérateur est nul :++:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 22 Juil 2010, 12:10
par Dinozzo13 » 22 Juil 2010, 12:10
Qmath a écrit:Cétait pas

? :zen:
Oui, il a raison, attention Lostounet
-
Anonyme
 par Anonyme » 22 Juil 2010, 12:16
par Anonyme » 22 Juil 2010, 12:16
On obtient alors:
=\frac{81}{a^4}+\frac{108}{a^3}-\frac{99}{a^2}-\frac{36}{a}+9)
= \frac{9P(a)}{a^4})
ce qui conclue la demo.
Au fait Dinozzo sait tu doù peut provenir ce
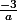
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 22 Juil 2010, 12:45
par Dinozzo13 » 22 Juil 2010, 12:45
Alors je savais en construisant cette énoncé, mais je ne sais plus trop maintenant.
Mais il me semble que cela a un rapport avec le +9 du P(x).
Car j'ai déjà vu et fait ce genre d'exo avec -2/a par exemple.
Par contre ce que je suis sur, c'est que concernant le coefficient des termes en x², peu importe la valeur qu'on lui attribue, alors ca marche aussi.
ex : soit m un paramètre réel, il me semle donc que si a est racine de x^4-4x^3+mx^2+12x+9 alors -3/a l'est aussi.
Mais, je chercherai concerant la provenance de -3/a :++:
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 22 Juil 2010, 13:04
par beagle » 22 Juil 2010, 13:04
si cela se trouve ton polynome puissance 4 est le produit de 2 polynomes puissance 2, avec (...+...+3)(...+...+3)
et on a appris au collège avec ton exo que la soluce, si soluce a alors -3/a soluce,
sauf que t'as lachement laissé tomber les collégiens sans dire-expliquer pourquoi trois quoi.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Juil 2010, 13:30
par Ben314 » 22 Juil 2010, 13:30
En fait, la "méthode" préconisés par Dinozzo marche pour tout polynôme
=ax^4+bx^3+cx^2+dx+e)
tel que
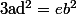
(et effecivement
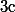
quelconque)
Ca marcherais aussi pour tout polynôme
=ax^5+bx^4+cx^3+dx^2+ex+f)
tel que
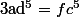
et
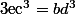
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 22 Juil 2010, 13:51
par Dinozzo13 » 22 Juil 2010, 13:51
Voilà, j'ai sorti mon joker ^^
Oui, et de plus cela a un rapport aussi avec le fait que quand on calcule P(-3/a) on retrouve le polynôme P mais les coefficient sont retrouvés dans l'ordre inverse
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 23 Juil 2010, 10:34
par Dinozzo13 » 23 Juil 2010, 10:34
Puisqu'on est en ce moment dans les polynômes, je propose un autre exo dessus :
Soit
)
le polynôme suivant :
=x^3+2x^2-5x-6)
On suppose que
)
admet trois racines distinctes
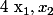
et
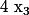
1°) Montrer qu'il est possible de déterminer :
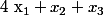
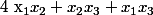
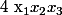
Sans calculer les racines.
En déduire la valeur de :


-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 23 Juil 2010, 14:04
par Olympus » 23 Juil 2010, 14:04
1°)
Soient
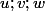
les trois racines ( réelles ou non ) de notre polynôme .
On a
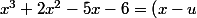 \left( x-v \right) \left( x-w \right))
Or, il est facile de vérifier que
 \left( x-v \right) \left( x-w \right) = x^3 - \left( u + v + w \right) x^2 + \left( uv+vw+wu \right)x - uvw)
.
Donc
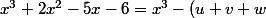 x^2 + \left( uv+vw+wu \right)x - uvw)
.
Par identification, on aura :
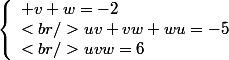
Or, comme 0 n'est pas une racine de notre polynôme,
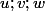
sont donc non-nulles .
On a
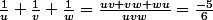
.
CQFD .
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 24 Juil 2010, 10:47
par Dinozzo13 » 24 Juil 2010, 10:47
Encore un autre ^^
Soit
)
le polynôme de paramètre réel
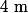
non nul défini par :
=x^4-\(\frac{1}{m^2}+m^2\)x^2+1)
1°) Déterminer, suivant les valeurs du réel non nul
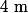
, le nombre de racine de
)
2°) Factoriser
)
3°) Pour quelle(s) valeur(s) de
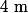
non nul :
a)
)
admet une racine quadruple
b)
)
est le carré d'un trinôme.
joli
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 24 Juil 2010, 10:54
par Dinozzo13 » 24 Juil 2010, 10:54
J'en rajoute un petit ^^
Déterminer les réels
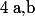
et
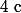
pour que le polynôme

défini par :
=x^6+ax^4+10x^3+bx+c)
, admet une racine quadruple.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 24 Juil 2010, 10:57
par Dinozzo13 » 24 Juil 2010, 10:57
Entre parenthèse, petite question :
Est-ce que tout les polynôme à coefficients symétriques de degré

, admettent toujours

racines ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Juil 2010, 11:45
par Ben314 » 24 Juil 2010, 11:45
Des racines dans R ou dans C ?
Si c'est dans R, le polynôme P(x)=x^n+1 (qui est bien à coeff symétriques) montre qu'il peut n'y avoir que trés peu de racines réelles.
Sinon, le polynôme (x+1)^n (qui est à coeff symétriques) admet lui aussi "peu" de racines, même dans C...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 24 Juil 2010, 11:54
par Dinozzo13 » 24 Juil 2010, 11:54
Ah oui, pas bête :ptdr: donc : non, pas nécessairement
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
