Pour (re)reprendre concernant l'importance de "maitriser qui est quoi" dans les formules qu'on écrit, j'ai bien l'impression que, dans tout ce que tu as écrit comme formules, un truc "qui t'échappe", c'est qu'
on veut que ce soit vrai pour absolument n'importe quel réel x.
Par exemple, dés le tout début, à savoir là :
yann06 a écrit: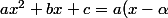^{2}+ \beta)
Tu peut parfaitement dire que, vu que ça doit être vrai
pour n'importe quel x, il faut par exemple que ce soit vrai pour x=0, c'est à dire que l'on doit
forcément avoir 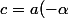^{2}+ \beta)
.
Et, ça doit aussi être vrai pour

ce qui te dit que l'on doit
forcément avoir 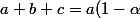^{2}+ \beta)
etc etc...
Le problème, c'est que, même si tu écrit 36 égalités de la sorte, c'est pas clair que ce soit
équivalent à l'équation de départ : si tu écrit juste que le truc doit être vrai pour x=0, pour x=1, pour x=2 et pour x=3, ça ne prouve à priori pas qu'il va aussi être vrai pour x=4. Donc il ne faut pas
uniquement procéder ainsi (mais c'est super utile de prendre conscience du fait que, si un truc doit être vrai pour tout les x, ben il doit être vrai pour x=0, x=1, etc...)
Sinon, la bonne façon de procéder, c'est effectivement de développer :
^{2}+ \beta=ax^2-2a\alpha x+a\alpha^2+\beta)
puis de dire que, pour que ce truc soit égal à
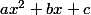 pour n'importe quel x réel
pour n'importe quel x réel, il suffit (*) qu'on ait

et

et tu n'a plus qu'à résoudre.
(*) En fait c'est un "il faut et il suffit".
Pour montrer le "il faut", partant de
^{2}+ \beta=ax^2-2a\alpha x+a\alpha^2+\beta) pour tout x
pour tout x, on peut commencer par prendre x=0 ce qui fait qui donne

puis prendre x=1 ce qui donne, après un mini calcul,

.
@zygo : merci pour les "éclaircissement". J'en profite pour rappeler que je suis "un vieux c..." et qu'en fait j'en ait plus grand chose à f...
MAIS ton intermédiaire entre 4) et 5) m'incite à (re)préciser qu'il ne faut pas trop voir une critique dans mes intervention de ce type : quand je vois les copies des M1 enseignement qui ont passés 3 ans chez nous, il ressort assez clairement qu'on a pas trop de leçons à donner à qui que ce soit... (évidement, c'est "en moyenne" : il y en a heureusement certains qui ont assimilés pas mal de trucs)

