Bonjour,
voilà l'intitulé du problème :
Trouver le reste de la division de P(x) = x^n + x + 1 par (x-1)² où n est un entier naturel supérieur ou égale à 2 .
Je pensais m'aider de congruence ou d'un raisonnement par récurrence mais ça ne me donne rien...
voilà merci pour votre aide
Reste d'une division de polynomes
4 messages
- Page 1 sur 1
Salut,
Le reste de la division d'un polynôme par (x-1)² (qui est de degré 2) est forcément de degré strictement plus petit que 2.
Tu peut donc écrire que :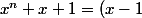^2Q(x)+ax+b) et, ce que tu cherche, c'est
et, ce que tu cherche, c'est  et
et  et tu n'a rien à faire de Q (qui est le quotient).
et tu n'a rien à faire de Q (qui est le quotient).
Un idée assez facile pour "faire disparaitre Q", c'est de prendre x=...
Une idée un peu plus astucieuse, lièe au fait que le (x-1) est au carré consiste à commencer par dériver la relation puis à remplacer x par ...
P.S. : tu peut aussi évaluer le reste pour n=2, n=3, n=4, n=5,... jusqu'à ce que tu "voie" quelle est la formule générale puis, tu démontre ta conjecture en faisant une récurrence.
Le reste de la division d'un polynôme par (x-1)² (qui est de degré 2) est forcément de degré strictement plus petit que 2.
Tu peut donc écrire que :
Un idée assez facile pour "faire disparaitre Q", c'est de prendre x=...
Une idée un peu plus astucieuse, lièe au fait que le (x-1) est au carré consiste à commencer par dériver la relation puis à remplacer x par ...
P.S. : tu peut aussi évaluer le reste pour n=2, n=3, n=4, n=5,... jusqu'à ce que tu "voie" quelle est la formule générale puis, tu démontre ta conjecture en faisant une récurrence.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Comme souvent, on ne vois pas bien car on écrit (comme je l'ai moi même fait) :
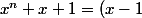^2Q(x)+ax+b)
alors que, pour rédiger "super propre", on devrait systématiquement écrire :
Pour tout réel x, on a (ou plutôt "on veut que")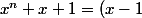^2Q(x)+ax+b)
Phrase dans laquelle il est beaucoup plus clair que l'on peut prendre x=... ou bien x=...
alors que, pour rédiger "super propre", on devrait systématiquement écrire :
Pour tout réel x, on a (ou plutôt "on veut que")
Phrase dans laquelle il est beaucoup plus clair que l'on peut prendre x=... ou bien x=...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
