Bonjour,
je me permet de demander votre aide car je cherche à résoudre l’équation 4x^2-35-9/x^2 =0.
Peut-être puis-je dire que 9/x^2 revient à 1/9x^2 mais je ne sais pas si bgn’est vrai.
Je sais qu’il faut que je calcule le déterminant delta de l’équation or j’ai besoin de connaître à,b et c mais je ne sais pas passer l’équation sous la forme ax^2+bx+c.
Pourriez-vous m’aider ?
merci
Résoudre une équation du second degré
3 messages
- Page 1 sur 1
Re: résoudre une équation du second degré
Bonjour ;
Tu as :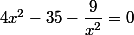 ; donc en mettant le tout au même dénominateur ,
; donc en mettant le tout au même dénominateur ,
tu auras :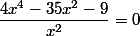 ;
;
donc te voilà très proche de ton :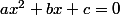 .
.
Tu as :
tu auras :
donc te voilà très proche de ton :
Re: résoudre une équation du second degré
Bonjour,
je rajoute une petite indication : on posera par exemple y = x^2, et on résoudra l'équation du second degré en y (en ne gardant que les solutions en y >= 0 car y est un carré), puis on remontera aux solutions en x de l'équation de départ..
Les équations du type de 4x^4-35x^2-9 s'appellent équations bicarrées et peuvent être toutes traitées de cette façon
je rajoute une petite indication : on posera par exemple y = x^2, et on résoudra l'équation du second degré en y (en ne gardant que les solutions en y >= 0 car y est un carré), puis on remontera aux solutions en x de l'équation de départ..
Les équations du type de 4x^4-35x^2-9 s'appellent équations bicarrées et peuvent être toutes traitées de cette façon
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 97 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
