Résoudre un système d'équations avec deux inconnues

[Amanote90]

Bonsoir,
Je n'arrive pas du tout à résoudre ce système d'équations. Je sais que à la fin je dois parvenir à x=2 et y=-1, mais je ne sais pas comment obtenir ce résultat.
J'ai essayé de exprimer y en fonction de x et vice-versa puis les remplacer dans l'équation... mais ça me fait des calculs très longs et je ne parviens jamais au bon résultat, c'est toujours des nombres décimaux que j'obtiens.




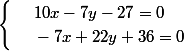
Merci d'avance

[BB27]

Tu multiplies la première équation par 7 et la deuxième par 10, tu additionnes les résultats, tu te retrouveras avec une équation à une inconnue (y). Tu la résous et ensuite tu remplaces la valeur de y obtenue dans une des équations du départ. Bonne chance.

[Amanote90]

Tu multiplies la première équation par 7 et la deuxième par 10, tu additionnes les résultats, tu te retrouveras avec une équation à une inconnue (y). Tu la résous et ensuite tu remplaces la valeur de y obtenue dans une des équations du départ. Bonne chance.

Merci beaucoup, j'y suis arrivé maintenant!

[LB2]

Bonsoir,

interprétation géométrique: dans le plan repéré (0,i,j), il s'agit de déterminer l'intersection de deux droites affines non parallèles. On obtient donc un unique point d'intersection, c'est à dire une unique solution/

[Amanote90]

Bonsoir,

interprétation géométrique: dans le plan repéré (0,i,j), il s'agit de déterminer l'intersection de deux droites affines non parallèles. On obtient donc un unique point d'intersection, c'est à dire une unique solution/

Oh je le vois maintenant, merci!