Résoudre Polynôme complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Le_Doc
- Membre Naturel
- Messages: 19
- Enregistré le: 26 Sep 2012, 16:57
-
 par Le_Doc » 26 Sep 2012, 20:43
par Le_Doc » 26 Sep 2012, 20:43
Bonjour,
Je suis à un numéro qui demande d'abord d'écrire en facteurs linéaires ou quadratiques irréductibles réels et également de donner les racines de l'expression suivante:

Bon, du coup, j'arrive à comprendre que je peux commencer par faire

^4 = 81 ?)
Mais par la suite, c'est un peu le néant, je suis tanné de ne pas comprendre ce que je fais lorsque je fais ce genre de problème, j'aimerais comprendre une bonne fois pour tout comment faire la mécanique de ce problème. Tout aide sera très apprécié ! Merci
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 26 Sep 2012, 20:46
par Luc » 26 Sep 2012, 20:46
Salut,
il y a deux façons d'écrire un nombre complexe. Sous forme algébrique (Partie réelle +i partie imaginaire) ou sous forme exponentielle (module/argument). A ton avis, quelle est la plus adaptée ici?
Et ne vois tu pas une solution "évidente" en nombres entiers à cette équation?
-
Le_Doc
- Membre Naturel
- Messages: 19
- Enregistré le: 26 Sep 2012, 16:57
-
 par Le_Doc » 26 Sep 2012, 20:52
par Le_Doc » 26 Sep 2012, 20:52
Évidemment que
z = 3
C'est à partir de ce point que je ne sais plus comment m'y prendre. J'ai toujours de la difficulté dès que l'on dépasse le bornes -1 .. +1 du cercle trigo pour trouver les angles. Alors j'imagine que c'est plus simple d'écrire dans ce cas quelque chose comme
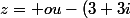)
Est-ce que je me trompe ? Il y a possibilité de quatre racines de la sorte.. je crois ..
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 26 Sep 2012, 21:03
par Luc » 26 Sep 2012, 21:03
Le_Doc a écrit:Évidemment que
z = 3
Ok.
Et

, tu saurais résoudre?
-
Le_Doc
- Membre Naturel
- Messages: 19
- Enregistré le: 26 Sep 2012, 16:57
-
 par Le_Doc » 26 Sep 2012, 21:07
par Le_Doc » 26 Sep 2012, 21:07
Luc a écrit:Ok.
Et

, tu saurais résoudre?
Non, je suis embêté je dois avouer. . . d'où mon besoin de comprendre un peu la méthode de résolution.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 26 Sep 2012, 21:25
par Luc » 26 Sep 2012, 21:25
Le_Doc a écrit:Non, je suis embêté je dois avouer. . . d'où mon besoin de comprendre un peu la méthode de résolution.
Il faut utiliser la forme exponentielle module/argument et trouver une équation simple pour l'argument.
-
Le_Doc
- Membre Naturel
- Messages: 19
- Enregistré le: 26 Sep 2012, 16:57
-
 par Le_Doc » 26 Sep 2012, 22:19
par Le_Doc » 26 Sep 2012, 22:19
Donc, si je saisie moindrement après un peu de temps de réflexion :

Donc;
^4 = 1*e^{i(0 + 2k\pi/2)})
0 ici à cause que 1 = cos 0 + isin0, vrai?
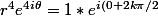})


De là,
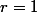

Donc la je ne sais plus où aller par contre ! :doh:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
