Résoudre inéquation seconde
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 05 Fév 2012, 20:17
par Shew » 05 Fév 2012, 20:17
wakaloup35 a écrit:oulà effectivement, a²-2ab+b²=(a-b)² ^^
donc (x-1)²=0
(x-1)(x-1)=0
x-1=0
x=1
c'était ça ?
Bravo c'etait bien ça

-
wakaloup35
- Membre Relatif
- Messages: 137
- Enregistré le: 01 Nov 2011, 16:34
-
 par wakaloup35 » 05 Fév 2012, 20:26
par wakaloup35 » 05 Fév 2012, 20:26
Shew a écrit:Bravo c'etait bien ça

Encore une chose :
On me demande graphiquement de résoudre g(x) < ou = à f(x)
S = [1;+infini[
c'est bien ça ?
Et par le calcul, on fait comment ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 05 Fév 2012, 20:52
par Shew » 05 Fév 2012, 20:52
wakaloup35 a écrit:Encore une chose :
On me demande graphiquement de résoudre g(x) < ou = à f(x)
S = [1;+infini[
c'est bien ça ?
Et par le calcul, on fait comment ?
Par ou tend g(x) quand

?
-
wakaloup35
- Membre Relatif
- Messages: 137
- Enregistré le: 01 Nov 2011, 16:34
-
 par wakaloup35 » 05 Fév 2012, 21:02
par wakaloup35 » 05 Fév 2012, 21:02
Shew a écrit:Par ou tend g(x) quand

?
euh décroissante ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 05 Fév 2012, 21:12
par Shew » 05 Fév 2012, 21:12
wakaloup35 a écrit:euh décroissante ?
D'accord mais g(x) est il positif ou negatif quand

?
-
wakaloup35
- Membre Relatif
- Messages: 137
- Enregistré le: 01 Nov 2011, 16:34
-
 par wakaloup35 » 05 Fév 2012, 21:14
par wakaloup35 » 05 Fév 2012, 21:14
Shew a écrit:D'accord mais g(x) est il positif ou negatif quand

?
euh g(x) est négatif sur [0;+infini[
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 05 Fév 2012, 21:20
par Shew » 05 Fév 2012, 21:20
wakaloup35 a écrit:euh g(x) est négatif sur [0;+infini[
Pour g(x) calculez :
g(-3)
g(-5)
g(-15)
g(-25)
Qu'en deduisez vous ?
-
wakaloup35
- Membre Relatif
- Messages: 137
- Enregistré le: 01 Nov 2011, 16:34
-
 par wakaloup35 » 05 Fév 2012, 21:59
par wakaloup35 » 05 Fév 2012, 21:59
Shew a écrit:Pour g(x) calculez :
g(-3)
g(-5)
g(-15)
g(-25)
Qu'en deduisez vous ?
g(-3)=-2*-3-1
g(-3)=5
g(-5)=-2*-5-1
g(-5)=9
g(-15)=-2*-15-1
g(-15)=29
g(-25)=49
je vois pas ce qu'il faut déduire et quel est le rapport avec g(x)<ou=f(x) ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 05 Fév 2012, 22:00
par Shew » 05 Fév 2012, 22:00
wakaloup35 a écrit:g(-3)=-2*-3-1
g(-3)=5
g(-5)=-2*-5-1
g(-5)=9
g(-15)=-2*-15-1
g(-15)=29
g(-25)=49
je vois pas ce qu'il faut déduire
Et bien quand x est negatif , g(x) est ???
-
wakaloup35
- Membre Relatif
- Messages: 137
- Enregistré le: 01 Nov 2011, 16:34
-
 par wakaloup35 » 05 Fév 2012, 22:01
par wakaloup35 » 05 Fév 2012, 22:01
Shew a écrit:Et bien quand x est negatif , g(x) est ???
positif mais quel rapport avec g(x)<ou=f(x) ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 05 Fév 2012, 22:17
par Shew » 05 Fév 2012, 22:17
wakaloup35 a écrit:positif mais quel rapport avec g(x)<ou=f(x) ?
Vous connaissez la valeur de x lorsque f(x) = g(x) , quand
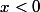
g(x) est positif , donc comment l'exprimer ?
-
wakaloup35
- Membre Relatif
- Messages: 137
- Enregistré le: 01 Nov 2011, 16:34
-
 par wakaloup35 » 05 Fév 2012, 22:29
par wakaloup35 » 05 Fév 2012, 22:29
[quote="Shew"]Vous connaissez la valeur de x lorsque f(x) = g(x) , quand [TEX] x =0
(x-1)²>=0
(x-1)(x-1)>=0
x>=1
On sait que Cg coupe Cf au point d'abscisse x=1 et que Cg est négatif sur ]0;+infini[ donc g(x)<=f(x) pour x appartenant à [1;+infini[
Est-ce bien ça ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 05 Fév 2012, 23:05
par Shew » 05 Fév 2012, 23:05
wakaloup35 a écrit:Je dois faire un calcul ?
-2x-1=0
(x-1)²>=0
(x-1)(x-1)>=0
x>=1
On sait que Cg coupe Cf au point d'abscisse x=1 et que Cg est négatif sur ]0;+infini[ donc g(x)<=f(x) pour x appartenant à [1;+infini[
On cherche a definir la tendance de la fonction g(x) tel que
 \le f(x))
, on sait que g(x) = f(x) quand x = 1 . On a vue que g(x) etait positive quand x < 0 donc x est positif quand

. Il ne vous reste plus qu'a definir quand
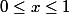
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités