Bonjour,
J'aimerai résoudre un système d'équations pour lequel je bloque, à l'aide d'un trinôme du second degré si possible, et des connaissances de première S. Voici le système.
x+y=13
(10x+y)(10y+x)=4930
Pouvez vous m'expliquer les calculs demandés en détail étape par étape ?
Merci
Résolution système d'équations à deux inconnues
9 messages
- Page 1 sur 1
Salut !
Prends la première équation, exprime y en fonction de x.
Ensuite, dans la deuxième équation, remplace y l'expression obtenue précédemment à partir de la première équation :++:
eb2108 a écrit:Bonjour,
J'aimerai résoudre un système d'équations pour lequel je bloque, à l'aide d'un trinôme du second degré si possible, et des connaissances de première S. Voici le système.
x+y=13
(10x+y)(10y+x)=4930
Pouvez vous m'expliquer les calculs demandés en détail étape par étape ?
Merci
Prends la première équation, exprime y en fonction de x.
Ensuite, dans la deuxième équation, remplace y l'expression obtenue précédemment à partir de la première équation :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
eb2108 a écrit:Y=13-x
Et je trouve -81x^2+1053x+1690=4930 soit -81x^2+1053x-3240=0
Est ce correct jusqu'ici ? Je sais que le résultat est 8 et 5 mais je ne sais pas comment le trouver. Si l'équation que je viens de poser est juste, je pourrai continuer seul ensuite
Merci
Divisez votre resultat par -81 .
]Propriété
deux nombres x et y sont déterminés (connus) ssi on connait leur produit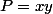
et leur somme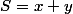
en effet x et y sont solutions de l'équation d'inconnue z
(z-y)=0)
en développant
z+xy=0)
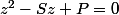
on résoud pour trouver x et y
J'ai appliqué cette méthode à ton système avec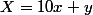 et
et 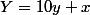 ,
,
la 1ere égalité permet, en multipliant par 10 de déterminer X+Y
deux nombres x et y sont déterminés (connus) ssi on connait leur produit
et leur somme
en effet x et y sont solutions de l'équation d'inconnue z
en développant
on résoud pour trouver x et y
J'ai appliqué cette méthode à ton système avec
la 1ere égalité permet, en multipliant par 10 de déterminer X+Y
J'ai trouvé la réponse en résolvant l'équation suivante.
Y=13-x
(10x+y)(10y+x)=4930
On développe la deuxième égalité en remplaçant y. On trouve le trinôme suivant qu'on résoud ensuite.
-81x^2+1053x+1690=4930 soit -81x^2+1053x-3240=0
Ce qui donne au final x=5
Et on remplace 5+y=13 ce qui donne y=8.
Merci de ton aide
:)
Y=13-x
(10x+y)(10y+x)=4930
On développe la deuxième égalité en remplaçant y. On trouve le trinôme suivant qu'on résoud ensuite.
-81x^2+1053x+1690=4930 soit -81x^2+1053x-3240=0
Ce qui donne au final x=5
Et on remplace 5+y=13 ce qui donne y=8.
Merci de ton aide
:)
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
