Résolution polynome

[shoupy77]

bonjour,

Je dois trouver les 3 valeurs a,b,c afin que les équations suivantes soient vraies :

a + b * cos (X1 + c ) = Y1
a + b * cos (X2 + c ) = Y2
a + b * cos (X3 + c ) = Y3
a + b * cos (X4 + c ) = Y4
a + b * cos (X5 + c ) = Y5
a + b * cos (X6 + c ) = Y6

Dans chaque équation, Xn et Yn sont connus.
Merci d'avance

[Elsa_toup]

Si tu as les valeurs Xn et Yn, c'est pas un problème...
Je numérote les équations de 1 à 6.

Dans 1, tu isoles a, que tu remplaces dans 2,3,4,5,6.
Puis tu ne touches plus à 1.

Dans 2, tu isoles b, que tu remplaces dans 3,4,5,6.

Tu as donc 4 équations avec seulement c comme inconnue. Comme il est question des fonctions cosinus ici, je pense qu'il te suffira de la 3 et la 4 pour obtenir c.

En fait, si tu pouvais me donner les valeurs de X et Y, je vérifierais cela.

[shoupy77]

valeurs pour Xn et Yn :

X1 = 0 ; Y1 = -276

X2 = 30 ; Y2 = -128

X3 = 60 ; Y3 = 83

X4 = 90 ; Y4 = 299

X5 = 120 ; Y5 = 464

X6 = 150 ; Y6 = 532

Voilà comme convenue

[Elsa_toup]

Le raisonnement est très simple, mais ultra long à recopier.
C'est comme je te l'ai dit plus haut (méthode du pivot de Gauss).

Vue la manière dont le problème est posé, j'imagine qu'il ne s'agit pas de Maths, mais plus vraisemblablement de Physique (3 équations auraient suffi, un problème de Maths n'en auraient pas donné plus... pas fous les Matheux !!! lol).

Donc je te livre les réponses. Si vraiment tu as besoin des explications, je te les donnerai bien sûr:
(les valeurs sont approchées au centième)
a = 107,12
b = - 429,14
c = 26,78

[shoupy77]

je vois que tu es costaud en maths.

Je constate que tes résultat sont juste car j'étais arrivé à

a =105
b= -428
c=27

en faisant à approche successive, donc pas assez satisfaisant.

Je suis donc très intéressé par tes explications afin de comprendre exactement la procédure afin de la répéter pour d'autres séries d'équations simiulaires*

Un grand Merci

[shoupy77]

j'ai regardé la méthode du pivot de Gauss. J'ai essayé de m'en sevir pour résoudre mes équations mais avec le produit du "cos" au milieu je n'arrive pas à m'en sortir.

[Elsa_toup]

Bon je t'avais écrit un long message mais tout a planté.
Alors je te fais la version courte: dans ta 3ème équation (tu n'as besoin que des 3 premières), tu tombes sur des termes en (par exemple) : cos(c+30)-cos(c).
Du coup, il faut utiliser la formule : cos(c+x)=cos(c)*cos(x)-sin(c)*sin(x).
En sachant que cos(60)=1/2=sin(30) et sin(60)=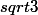/2 =cos(30), tu tombes sur les résultats.

Ah oui, à la fin, tu as sin(c)/cos(c). C'est égal à tan(c).
Donc tu as tan(c)=y (où y est un nombre à coucher dehors).
Tu fais alors : c =arctan (y), sur ta calculatrice, et c'est bon !!!

Manifeste-toi si tu bloques...

[shoupy77]

Je vais voir si j'arrive à trouver en faisant comme tu dis. Demain je tiens au courant si j'y suis arrivé.

Au cas où j'essayerais de te joindre. Si tu veux m'envoyer un mail direct, tu peux à : f.baille@technoconcept.fr

Merci , bonne soirée

[shoupy77]

j'ai essayé de résoudre mon problème comme tu me l'a expliqué à partir des 3 premieres equations mais je n'arrive pas a obtenir le sin x / cos x.

Si tu peux m'aider c'est volontier. Merci d'avance

[Elsa_toup]

Ok alors tu as : a = -276 - b*cos(c)

Donc (2) donne : b = 148 / [cos(c+30)-cos(c)]

Donc (3) devient : 148 [cos(c+60)-cos(c)] = 359 [cos(c+30)-cos(c)]

donc : 148 [cos(c)*cos(60) - sin(c)*sin(60) - cos(c)] = 359 [cos(c)*cos(30) - sin(c)*sin(30) - cos(c)]

soit: 148 [cos(c)/2 - (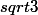/2)sinc(c) - cos(c)] = 359 [(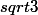/2)cos(c) - sin(c)/2 - cos(c)]

donc : 148 [(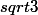/2)sinc(c) - cos(c)/2] = 359 [(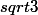/2 - 1)*cos(c) - sin(c)/2]

Je multiplie à gauche et à droite par 2 (pour enlever les fractions) et je développe:

148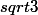 sin(c) + 148 cos(c) = 359 sin(c) + 359(2-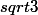)cos(c)

Je mets tous les sinus à gauche et les cosinus à droite, donc:
(359-148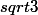)*sin(c) = (-570+359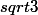)*cos(c)

Je fais passer le cos(c) à gauche (en divisant par cos(c)) et la parenthèse qui multiplie sin(c) à droite:
sin(c)/cos(c) = (-570+359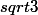) / (359-148)

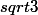Sin/cos=tan, donc (je note N la fraction immonde à droite):
tan(c) = N

et, c = arctan (N)

Tu calcules ça sur ta calculatrice (arctan doit être la touche "Atn", je pense)
et tu en déuis a et b.

[shoupy77]

OK pour tes explications que j'ai bien compris. Là dans l'exemple que tu m'a fais tu te base sur les 3 premieres équations et en particulier sur la première où X1=0, ce qui fait donc cos( c ).

Mais si on prend les équations par exemples 2,3,4 où il y a toujours une valeur Xn alors ca deviens insoluble, non ?

[Elsa_toup]

Si, c'est tout à fait possible.
A partir du moment où tu as 3 équations à 3 inconnues, tu peux résoudre le système.

Il suffit d'exprimer la 1ère inconnu en fonction des 2 autres, puis de reporter.
Il te reste alors 2 inconnues dans 2 équations. Tu exprimes l'une en fonction de l'autre et tu reportes dans la dernière équation: tu as une équation à une inconnue.

Par exemple, avec tes équations (2), (3) et (4), j'obtiens, à la dernière ligne:

[191 + 427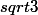 /2] * sin(c) = [236 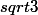- 427/2] * cos(c).

Quand tu en es là, tu résouds comme dans le cas que je t'ai exposé plus haut.

[shoupy77]

Avec tes explications je suis arrivé à comprendre le processus pour obtenir les valeurs de a,b,c .
Tu es génial.
Actuellement je vais mettre tout cà en forme dans un tableau excel afin de trouver l'équation pour chacun de mes relevés de valeurs.
Merci, bye