Resolution d'équations/inéquations
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 13:18
par Dante0 » 01 Avr 2012, 13:18
Iroh a écrit:Oui
Le message que vous avez entré est trop court. Veuillez l'allonger à au moins 10 caractères.
Merci ! :p
Un autre exercice :
Je dois différencier ces 2 equations :
 = (\frac{2x}{x+2})^4)
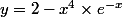
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 13:35
par Iroh » 01 Avr 2012, 13:35
Dante0 a écrit:Merci ! :p
Un autre exercice :
Je dois différencier ces 2 equations :
 = (\frac{2x}{x+2})^4)
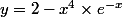
Pour le premier,
)^n = n (g(x))^{n-1} \frac{d}{dx} g(x))
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 14:04
par Dante0 » 01 Avr 2012, 14:04
Iroh a écrit:Pour le premier,
)^n = n (g(x))^{n-1} \frac{d}{dx} g(x))
Qu'est-ce que t'as fait ? :doh:
Tu peux me faire un briefing rapide ? J'ai jamais vu cette lecon et je l'ai au programme du concours que je dois passer.
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 14:18
par Iroh » 01 Avr 2012, 14:18
Dante0 a écrit:Qu'est-ce que t'as fait ? :doh:
Tu peux me faire un briefing rapide ? J'ai jamais vu cette lecon et je l'ai au programme du concours que je dois passer.
On demande juste de dériver les fonctions, non ?
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 14:30
par Dante0 » 01 Avr 2012, 14:30
Iroh a écrit:On demande juste de dériver les fonctions, non ?
L'énoncé exact : "Differentiate the following functions, simplify and factorize"
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 14:52
par Iroh » 01 Avr 2012, 14:52
Dante0 a écrit:L'énoncé exact : "Differentiate the following functions, simplify and factorize"
Oui, faut juste dériver.
T'as vu la formule pour dériver une composée de fonctions.
(x) = \frac{d}{dx} g(h(x)) = \frac{d}{d(h(x))}g(h(x))\frac{d}{dx}h(x))
Ça a l'air monstrueux, mais c'est assez simple en pratique.
On va prendre comme exemple la fonction
 = (3x)^5)
. Tu sais que la dérivée de
 = x^5)
c'est
 = 5x^4)
. Et que la dérive de
 = 3x)
c'est
 = 3)
. Tu remarque que
 = (g\circ h)(x))
.
Donc par la formule:
 &=& \frac{d}{d(3x)}(3x)^5\,\frac{d}{dx}3x\\<br />& = & (5)(3x^4)(3)\\ & =& 45x^4\end{eqnarray})
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 14:57
par Dante0 » 01 Avr 2012, 14:57
Iroh a écrit:Oui, faut juste dériver.
T'as vu la formule pour dériver une composée de fonctions.
(x) = \frac{d}{dx} g(h(x)) = \frac{d}{d(h(x))}g(h(x))\frac{d}{dx}h(x))
Ça a l'air monstrueux, mais c'est assez simple en pratique.
On va prendre comme exemple la fonction
 = (3x)^5)
. Tu sais que la dérivée de
 = x^5)
c'est
 = 5x^4)
. Et que la dérive de
 = 3x)
c'est
 = 3)
. Tu remarque que
 = (g\circ h)(x))
.
Donc par la formule:
 &=& \frac{d}{d(3x)}(3x)^5\,\frac{d}{dx}3x\\<br />& = & (5)(3x^4)(3)\\ & =& 45x^4\end{eqnarray})
Je suis pas du tout habitué à la notation mais ca revient bien à écrire :
' = f'(g(x))\times f(x))
?
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 14:59
par Iroh » 01 Avr 2012, 14:59
Dante0 a écrit:Je suis pas du tout habitué à la notation mais ca revient bien à écrire :
' = f'(g(x))\times f(x))
?
Non:
'(x) = f'(g(x))\times g'(x))
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 15:25
par Dante0 » 01 Avr 2012, 15:25
Iroh a écrit:Non:
'(x) = f'(g(x))\times g'(x))
Au temps pour moi.
Dans ce cas la réponse à la première c'est :
^3}{(x+2)^5})
?
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 15:28
par Iroh » 01 Avr 2012, 15:28
Dante0 a écrit:Au temps pour moi.
Dans ce cas la réponse à la première c'est :
^3}{(x+2)^5})
?
Oui c'est correct.
Pour la deux t'as juste un produit de fonction à dériver.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
. Tu sais que la dérivée de
c'est
. Et que la dérive de
c'est
. Tu remarque que
.