Resolution d'équations/inéquations
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 31 Mar 2012, 16:52
par Dante0 » 31 Mar 2012, 16:52
Bonjour,
J'ai un soucis avec ces équations/inéquations :
1)
 < 1)
2)
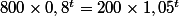
3)
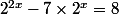
4)
e^{-0,5x^2} < 0)
Merci !

-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 31 Mar 2012, 17:16
par Iroh » 31 Mar 2012, 17:16
Salut,
D'abord tu peux exprimer les nombres décimaux sous forme de fractions.
Pour le premier, tu as besoin des formules :

} = \ln a+\ln b)
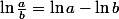
Pour le deuxième:
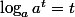
La troisième, pose
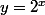
La quatrième, que vaut le signe d'un produit de fonctions ? Quel est le signe de la la fonction exponentielle.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 08:04
par Dante0 » 01 Avr 2012, 08:04
Comment peut-on écrire
 < 1)
différemment ?

?
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 01 Avr 2012, 08:26
par nodjim » 01 Avr 2012, 08:26
ln0.1x0
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 08:34
par Dante0 » 01 Avr 2012, 08:34
nodjim a écrit:ln0.1x0
Ok donc x < 20 ?
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 08:48
par Iroh » 01 Avr 2012, 08:48
Dante0 a écrit:Ok donc x < 20 ?
Oui correct.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 09:18
par Dante0 » 01 Avr 2012, 09:18
Iroh a écrit:Oui correct.
Ok pour la 2e, je dois passer en log ? J'ai pas compris ton explication.
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 09:24
par Iroh » 01 Avr 2012, 09:24
Dante0 a écrit:Ok pour la 2e, je dois passer en log ? J'ai pas compris ton explication.
Mets tout ce qui dépend de t d'un côté, après tu sais que
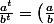^t)
, puis tu appliques la formule
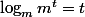
.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 10:21
par Dante0 » 01 Avr 2012, 10:21
Iroh a écrit:Mets tout ce qui dépend de t d'un côté, après tu sais que
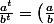^t)
, puis tu appliques la formule
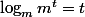
.
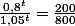
^t = ln4)
L'écriture en log m'embrouille complètement, j'ai pas appris mes formules comme ca.

-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 10:33
par Iroh » 01 Avr 2012, 10:33
Pas grave, tu peux t'en sortir en utilisant juste la fonction ln. Ici tu peux appliquer
 = t\ln x)
.
Par contre t'as fait une faute à la 2ème ligne. (200/800 = ?)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 10:38
par Dante0 » 01 Avr 2012, 10:38
Iroh a écrit:Pas grave, tu peux t'en sortir en utilisant juste la fonction ln. Ici tu peux appliquer
 = t\ln x)
.
Par contre t'as fait une faute à la 2ème ligne. (200/800 = ?)
Oups
Donc j'arrive à
 = ln\frac{1}{2})
Donc
} = \frac{\frac{1}{2}}{\frac{0,8}{1,05}})
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 10:43
par Iroh » 01 Avr 2012, 10:43
Dante0 a écrit:Oups
Donc j'arrive à
 = ln\frac{1}{2})
Donc
} = \frac{\frac{1}{2}}{\frac{0,8}{1,05}})
T'as du faire la fête hier soir ! :we: 200/800=?
T'as dernière égalité est fausse, tu ne peux pas simplifier le ln. Tu as la solution qui vaut
}{\ln(...)})
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 11:26
par Dante0 » 01 Avr 2012, 11:26
Iroh a écrit:T'as du faire la fête hier soir ! :we: 200/800=?
T'as dernière égalité est fausse, tu ne peux pas simplifier le ln. Tu as la solution qui vaut
}{\ln(...)})
Lol... :ptdr:
})
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 11:31
par Iroh » 01 Avr 2012, 11:31
Dante0 a écrit:Lol... :ptdr:
})
C'est ça,

-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 11:40
par Dante0 » 01 Avr 2012, 11:40
Iroh a écrit:C'est ça,

Ok ! Merci !

Pour la 3e à quoi ca m'avance de faire un changement de variable ?
Si je pose :

?
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 11:49
par Iroh » 01 Avr 2012, 11:49
Dante0 a écrit:Ok ! Merci !

Pour la 3e à quoi ca m'avance de faire un changement de variable ?
Si je pose :

?
Il faut poser
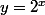
, pas
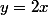
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 11:56
par Dante0 » 01 Avr 2012, 11:56
Iroh a écrit:Il faut poser
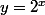
, pas
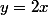
Ok je trouve
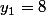
et
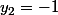
Donc

2^x = -1 x = impossible ?
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 12:02
par Iroh » 01 Avr 2012, 12:02
Dante0 a écrit:Ok je trouve
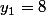
et
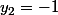
Donc

2^x = -1 x = impossible ?
Oui, qu'une seule solution réelle.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 01 Avr 2012, 12:30
par Dante0 » 01 Avr 2012, 12:30
Merci !

A présent la dernière :
e^{-0,5x^2} < 0)
L'exponentielle est toujours positive donc on doit résoudre x+1 < 0 ? Ce qui donne x < -1 ?
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 01 Avr 2012, 12:50
par Iroh » 01 Avr 2012, 12:50
Dante0 a écrit:Merci !

A présent la dernière :
e^{-0,5x^2} < 0)
L'exponentielle est toujours positive donc on doit résoudre x+1 < 0 ? Ce qui donne x < -1 ?
Oui
Le message que vous avez entré est trop court. Veuillez l'allonger à au moins 10 caractères.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités