Résolution équation - valeur absolue - complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Nov 2009, 22:47
par Dinozzo13 » 04 Nov 2009, 22:47
Bonsoir, j'ai souhaité résoudre dans
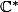
l'équation suivante :
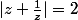
, mais je ne suis pas sûr de mon résultat, merci de m'aider en cas d'erreur.
Tout d'abord je résous
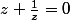
:
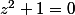
équivaut à
(z-i)=0)
d'où
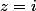
ou

Si

alors

, donc je résous
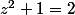
et par conséquent
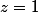
ou
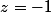
, d'où
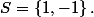
Si

alors

, donc je résous
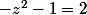
,
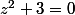
,
(z -i \sqrt 3)=0)
et par conséquent
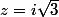
ou
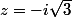
, d'où
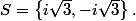

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 04 Nov 2009, 22:58
par Ericovitchi » 04 Nov 2009, 22:58
non ça va pas. Dans C dire

par exemple n'a pas de sens
remplaçes z par x+iy dans
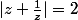
et tu verras qu'il y a une infinité de solutions situées sur une quartique
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 04 Nov 2009, 23:00
par Zweig » 04 Nov 2009, 23:00
Dinozzo13 a écrit:Si

alors

Je me suis arrêté là.
C'EST UNE ERREUR A NE PLUS REFAIRE ! (bon, pour la Terminale, on va dire que c'est pas si grave que ça, c'est nouveau pour toi les complexes). Sache que les relations d'ordre n'existent plus dans le corps des nombres complexes, tu ne peux pas dire qu'un nombre complexe est positif ou négatif, ou qu'un nombre complexe est plus grand ou plus petit qu'un autre.
Voici comment je procéderai :
|z+1/z| = 2 => |z+1/z|^2 = 4 (z+1/z)*conjugué(z+1/z)=4 |z|^2 + z/conj(z) + conj(z)/z + 1/|z|^2 = 4 z^4 + |z|^2(2*Re(z*conj(z))-4) + 1 = 0
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Nov 2009, 23:00
par Dinozzo13 » 04 Nov 2009, 23:00

mais après que faire ??? :doh:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Nov 2009, 23:02
par Dinozzo13 » 04 Nov 2009, 23:02
Zweig a écrit:C'EST UNE ERREUR A NE PLUS REFAIRE !.
Tant que t'es la pour les maths ^^
Zweig a écrit:(bon, pour la Terminale, on va dire que c'est pas si grave que ça, c'est nouveau pour toi les complexes).
:ptdr: ouais merci.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Nov 2009, 23:03
par Dinozzo13 » 04 Nov 2009, 23:03
Dinozzo13 a écrit:Tout d'abord je résous
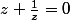
:
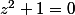
équivaut à
(z-i)=0)
d'où
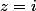
ou

Si

alors

, donc je résous
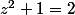
et par conséquent
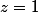
ou
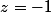
, d'où
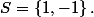
Si

alors

, donc je résous
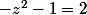
,
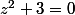
,
(z -i \sqrt 3)=0)
et par conséquent
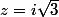
ou
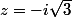
, d'où
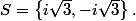
ouais donc tout ça sert à rien

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Nov 2009, 23:05
par Dinozzo13 » 04 Nov 2009, 23:05
Par contre, ça aurait été valable dans
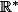
, non ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 05 Nov 2009, 11:37
par Ericovitchi » 05 Nov 2009, 11:37

|x+iy+(x-iy)/(x²+y²)|=2 --> |x+x/(x²+y²) + i (y-y/(x²+y²)|=2
--> x²(1+1/(x²+y²))² + y²(1-1/(x²+y²)² = 2
Ca ressemble à ça :

-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Nov 2009, 11:39
par benekire2 » 05 Nov 2009, 11:39
C'est beau les maths.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 05 Nov 2009, 15:29
par Zweig » 05 Nov 2009, 15:29
C'est la lemniscate de Bernoulli, non ?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 05 Nov 2009, 15:32
par Timothé Lefebvre » 05 Nov 2009, 15:32
Salut,
elle est pas couchée celle-là ? O_o
Enfin j'en sais rien, j'y connais rien !

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 05 Nov 2009, 15:34
par Ericovitchi » 05 Nov 2009, 15:34
Ca a un peu la même tronche mais je ne suis pas sûr
la lemniscate de bernouilli c'est
^2 = 2a^2 \times \left(x^2 - y^2\right))
ou en polaire
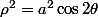
là ça a l'air un peu plus compliqué mais peut-être, j'ai la flegme de simplifier.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
alors