Resolution equation

[bobyoups]

Bonjour,

Quelqu'un serait t'il capable de resoudre l'equation :
ln x + 2/x - 1/(x^2) = 0
sur o;+infini

Merci beaucoup a tous ceux qui prendront le temps dy reflechir...

[fonfon]

Salut,

on pose f(x)=lnx+2/x-1/x²

tu etudies la fonction tu montres qu'elle est croissante sur ]0,+inf[

ensuite tu utilises le theoreme de bijection...

je vais être un peu plus complet:

Si la fonction est deivable sur I, on determine son tableau de variation.Lorsque la fonction est monotone sur un intervalle [a,b] de I et que f(a) et f(b) sont de signes contraires, alors il existe un seul nb réel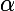 de ]a,b[ tel que

apres pour trouver alpha il faut que tu cherches un encadrement de la valeur à l'aide de ta calculatrice
A+

[nox]

waip d'accord avec le post ci-dessus. A moins qu'il y ait une astuce pour ce genre d'équation tu pourras pas trouver de valeur exacte.
Par contre pour trouver la valeur approchée il existe beaucoup de méthode (Newton, gradient conjugué, corde etc...).

Le plus souvent on utilise une dichotomie.

tu prends ton intervalle de départ (ca tend vers moins l'infini en 0 et en 1 ca vaut 1. Donc la fonction s'annule entre 0 et 1. On peut donc prendre [0 ; 1] comme intervalle de départ) puis tu le découpe en 2 sous-intervalles égaux [0 ; 1/2] et [1/2 ; 1]. Si en 1/2 la fonction est positive, elle s'annule entre 0 et 1/2. Si elle est négative, elle s'annule entre 1/2 et 1. Puis tu recommences avec le nouvel intervalle jusqu'a obtenir la précision souhaitée.

C'est la méthode la plus simple a mettre en oeuvre mais pas la plus rapide, surtout à programmer.

Pour les autres va voir sur :
http://fr.wikipedia.org/wiki/Algorithme_de_recherche_d'un_z%C3%A9ro_d'une_fonction