Résolution d'équation avec un x au carré

[sidney]

Bonjour , je bloque complètement sur une partie de mon exercice du coup j'espère que vous pourrez m'aider

Je dois résoudre l'équation x( x au cube - a)=0 en distinguant les cas où a est inférieur ou égal à 0 et a>0.
Je dois ensuite dresser son tableau de signes où on devra aussi distinguer les cas où a inférieur ou égal à 0 et a>0.

Voilà, toute aide est la bienvenue !

[Landstockman]

Bonjour,

On a déjà une solution évidente, .
On s'intéresse maintenant à l'éventualité où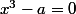
Que savez vous de la fonction qui a associe ?

D'ailleurs la disjonction de cas ne parait pas essentielle, êtes-vous sûre qu'il ne s'agit pas plutôt d'un ?

[samoufar]

D'ailleurs la disjonction de cas ne parait pas essentielle, êtes-vous sûre qu'il ne s'agit pas plutôt d'un ?

Ça serait d'ailleurs plus cohérent avec le titre du sujet

[sidney]

Bonjour,

On a déjà une solution évidente, .
On s'intéresse maintenant à l'éventualité où
Que savez vous de la fonction qui a associe ?

D'ailleurs la disjonction de cas ne parait pas essentielle, êtes-vous sûre qu'il ne s'agit pas plutôt d'un ?

Oui pardon, c'est x au carré !

[laetidom]

Bonjour,





que valent alors les solutions ?

[samoufar]

Bonjour,





que valent alors les solutions ?

Sous réserve d'avoir .

[laetidom]

Sous réserve d'avoir .

Oui effectivement !, merci samoufar de la précision !

[sarahbuebd]

est ce que tu pourrait m aider sur un devoir de proprtionnalité s il te plait