Résolution difficile sur exponentielle (ES)

[Eastern55]

Bonjour.
voila j'ai un exercice de mathematiques a faire mais l'inéquation est trop dure et je ne sais pas par quoi commencer.

Voici l'inéquation.

3e^x-1 < 4e^-x

Pourriez vous m'aider a resoudre cette équation en me donnant les étapes a franchir afin que je puisse la résoudre? merci beaucoup

[Arnaud-29-31]

Bonjour,

On pourra poser X = exp(x)

[Frednight]

ton inéquation équivaut à :

[Eastern55]

et je fais quoi avec ca? ^^' parce que je comprends pas tout la

[Frednight]

bah tu regroupes tes e^x sur un même côté tous seuls et t'applique un petit ln des deux côtés pour faire les faire sauter et voir quelle doit être la valeur de x

[gigamesh]

Bonsoir,
pas d'accord avec toi Frednight.
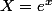
Il faut d'abord multiplier les deux membres par , ensuite poser et résoudre l'équation du second degré.

Ensuite, et ensuite seulement, des valeurs de X tu déduis les valeurs de x.