Réso d'équation avec racine dedans?
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 04 Nov 2009, 17:29
par eratos » 04 Nov 2009, 17:29
Salut!!
Voilà, je reprend doucement les maths pour me remettre à niveau en vue d'une reprise d'étude et d'obtention d'un daeu. J'en suis actuellement sur les polynômes du 2e degré et y a pas de soucis pour l'instant sauf un.
Je dois résoudre un petite équation du premier degré, et le résultat ne me convient pas. :mur:
= 2-x)
Donc:
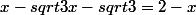
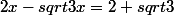
Maintenant je fais quoi? J'élève au carré?
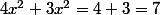

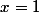

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 04 Nov 2009, 17:35
par Ericovitchi » 04 Nov 2009, 17:35
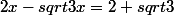
non tu n'élève pas au carré. Aucun intérêt.
Tu mets x en facteur, tu mets tout le reste de l'autre coté, tu divise les deux cotés par le facteur qui multiplie x, jusqu'à ce que tu tombes sur un x= ....
(PS et puis je te signale que quand tu élèves au carré tu oublies les doubles produits)
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 04 Nov 2009, 17:43
par oscar » 04 Nov 2009, 17:43
Bonjour Ce n' est PAS une équation du 2e degré
=> x -xV3 -v3 = 2-x
2x - x v3 = 2+v3
multiplier les deux de la fraction obtenue par le " conjugué de 2-v3
x = ......
-
fafa16
- Membre Naturel
- Messages: 48
- Enregistré le: 28 Avr 2009, 18:48
-
 par fafa16 » 04 Nov 2009, 17:59
par fafa16 » 04 Nov 2009, 17:59
oscar a écrit:Bonjour Ce n' est PAS une équation du 2e degré
=> x -xV3 -v3 = 2-x
2x - x v3 = 2+v3
multiplier les deux de la fraction obtenue par le " conjugué de 2-v3
x = ......
excusez moi pour le derangement mais oscar pourrais tu m'aider sur le probleme du 2nde degré merci d avance

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 04 Nov 2009, 18:29
par eratos » 04 Nov 2009, 18:29
Je ne comprend pas bien:

=2+ sqrt 3)
} {2-sqrt 3}= \frac {2+ sqrt 3} {2- sqrt 3})
Ici, je multiplie les deux termes par le conjugué de 2-V3 soit 2+V3?
Et les doubles produits, kézaco?
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 04 Nov 2009, 21:31
par oscar » 04 Nov 2009, 21:31
tu as x(2-V3) = 2+v3
x = ( 2+v3)/(2-v3)
x = (2+v3)(2+v3)/(2-v3)(2+v3)
Réduis et tu auras ainsi une belle réponse

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 05 Nov 2009, 07:58
par eratos » 05 Nov 2009, 07:58
OK :++:
Donc
(2+ sqrt3)}{(2- sqrt3)(2+ sqrt3)})
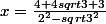
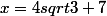
Merci en tout cas, va falloir que je retienne cette histoire.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités

