bonsoir, lorque l'on nous donne des suites genre Un=(-2)^n
comment faire sa représentation graphique ?
je sais qu'il faut calculer des termes. J'ai calculé les 5 premiers termes.
L'année dernière j'ai vu que je devais faire un axe tel que y=, mais il faut une autre information pour mettre les points non ? Il faut qu'on me donne une fonction non ? ( comme dans cet exemple là : http://www.mathforu.com/cours-93.html)
Représentation suite
7 messages
- Page 1 sur 1
Bonsoir,
Je ne vois aucune dificulté à tracer le graphique représentant une suite dont on donne le terme général.
C'est plus compliqué si l'on ne donne que le (ou les) premier(s) terme(s) et la relation de récurrence, comme dans l'exemple donné en réfèrence.
L'expresion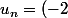^n) donne-t-elle le terme général de la suite oou est-ce une définition par récurrence ?
donne-t-elle le terme général de la suite oou est-ce une définition par récurrence ?
Je ne vois aucune dificulté à tracer le graphique représentant une suite dont on donne le terme général.
C'est plus compliqué si l'on ne donne que le (ou les) premier(s) terme(s) et la relation de récurrence, comme dans l'exemple donné en réfèrence.
L'expresion
C.Ret a écrit:Bonsoir,
Je ne vois aucune dificulté à tracer le graphique représentant une suite dont on donne le terme général.
C'est plus compliqué si l'on ne donne que le (ou les) premier(s) terme(s) et la relation de récurrence, comme dans l'exemple donné en réfèrence.
L'expresiondonne-t-elle le terme général de la suite oou est-ce une définition par récurrence ?
Il faut trouver la fonction donnant le terme de rang n+1 en fonction du terme de rang n.
Dans ce cas y=-2*x
Tracer les courbes y=-2*x et y=x, ce qui permet de trouver les termes succesifs de la suite comme indiqué dans la figure ci desous.
Rappelle si ce n'est pas assez clair

Et non, tout faux c'est l'inverse.
C'est bien cela que l'on appèle "relation par récurrence", car on obtient le terme de rang n+1 à partir du terme de rang immédiatement inférieur.
Cela s'exprime bien par une relation du type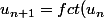)
Oui, mais pourquoi ne pas directement exprimer cela de cette façon : ?
?
Ou par lef ait que la suite est une suite géométrique de raison
est une suite géométrique de raison 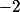 et de terme initial
et de terme initial 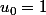 .
.
Ce qui n'est pas clair à mon avis c'est qu'il est bien plus simple de directement tracer la courbe en utilisant l'expression de définition générale :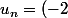^n)
On alors pas besoin de de la droite y=x, ni de reporter les valeurs des odonnées sur l'axe des abscisses.
Il suffit simplement de faire comme l'a indiqué Jocker62 en plaçant sur la figure les points de coordonnées) .
.
A savoir, directement les points (0,1); (1,-2); (2,4); (3,-8); (4,16); ...) ...
...
Je ne vois pas pourquoi faire compliquer pour une représentation aussi simple.
En fait, les suite sont en quelque sorte des fonctions :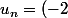^n) est à rapprochée de
est à rapprochée de  = (-2)^x) . La seule réelle diffèrence est le fait que n, contrairemtn à x, n'est pas définit de façon continue sur le domaine de définition.
. La seule réelle diffèrence est le fait que n, contrairemtn à x, n'est pas définit de façon continue sur le domaine de définition.
hammana a écrit:Il faut trouver la fonction donnant le terme de rang n+1 en fonction du terme de rang n.
C'est bien cela que l'on appèle "relation par récurrence", car on obtient le terme de rang n+1 à partir du terme de rang immédiatement inférieur.
Cela s'exprime bien par une relation du type
hammana a écrit:Dans ce cas y=-2*x
Oui, mais pourquoi ne pas directement exprimer cela de cette façon :
Ou par lef ait que la suite
hammana a écrit:Tracer les courbes y=-2*x et y=x, ce qui permet de trouver les termes succesifs de la suite comme indiqué dans la figure.
hammana a écrit:Rappelle si ce n'est pas assez clair
Ce qui n'est pas clair à mon avis c'est qu'il est bien plus simple de directement tracer la courbe en utilisant l'expression de définition générale :
On alors pas besoin de de la droite y=x, ni de reporter les valeurs des odonnées sur l'axe des abscisses.
Il suffit simplement de faire comme l'a indiqué Jocker62 en plaçant sur la figure les points de coordonnées
A savoir, directement les points (0,1); (1,-2); (2,4); (3,-8); (4,16); ...
Je ne vois pas pourquoi faire compliquer pour une représentation aussi simple.
En fait, les suite sont en quelque sorte des fonctions :
C.Ret a écrit:Et non, tout faux c'est l'inverse.
C'est bien cela que l'on appèle "relation par récurrence", car on obtient le terme de rang n+1 à partir du terme de rang immédiatement inférieur.
Cela s'exprime bien par une relation du type
Oui, mais pourquoi ne pas directement exprimer cela de cette façon :?
Ou par lef ait que la suiteest une suite géométrique de raison
et de terme initial
.
Ce qui n'est pas clair à mon avis c'est qu'il est bien plus simple de directement tracer la courbe en utilisant l'expression de définition générale :
On alors pas besoin de de la droite y=x, ni de reporter les valeurs des odonnées sur l'axe des abscisses.
Il suffit simplement de faire comme l'a indiqué Jocker62 en plaçant sur la figure les points de coordonnées.
A savoir, directement les points (0,1); (1,-2); (2,4); (3,-8); (4,16); ......
Je ne vois pas pourquoi faire compliquer pour une représentation aussi simple.
En fait, les suite sont en quelque sorte des fonctions :est à rapprochée de
. La seule réelle diffèrence est le fait que n, contrairemtn à x, n'est pas définit de façon continue sur le domaine de définition.
Je pense que le but du problème est de présenter la méthode graphique exposée dans le site
http://www.mathforu.com/cours-93.html)
Cette méthhode n'a aucun intérêt pour le cas très simple proposé, mais elle est très efficace pour répondre par exemple au problème suivant:
on considère la suite
montrer qu'elle converge vers 1 si
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
