Repère

par **nine** » 11 Oct 2006, 12:17

[CENTER]Bonjour[/CENTER]

J'ai un devoir maison à faire et je bloque à une question qui me parait facile mais à laquelle je n'arrive pas à repondre :mur:

_ Le plan est rapporté à un repère othonormal (O,i;j) d'unité 1cm.

Soit A(-1;0) I=2i-2j et J=2i+2j
Pouquoi (A,I,J) est-il un repère du plan?
[sur les "i" "I" "j" et "J" il y a la flèche des vecteurs]

svp est-ce-que vous pouvez m'aider!!!car je n'y arrive pas :cry:

MERCI

par **Roman** » 11 Oct 2006, 12:53

Bonjour,

nine, cherche dans ton cours : qu'est-ce qu'un repere du plan ?

Roman

par **fonfon** » 11 Oct 2006, 12:57

Salut, exprime les coordonnées de I et J et ensuite montre que 2 vecteurs (je te laisse les trouver) ne sont pas colineaires

par **nine** » 11 Oct 2006, 13:55

reuh :)

Mais je n'ai pas de cours sur les repères :doh:
je suis en 1re S et je pense que c'est des cours de 2nd mais je dois avouer que en 2nd je n'ai rien fait alors des trucs simple comme ca...bien ... je ne sais pas les faire :cry:

est-ce tu pourais alors me donner des indications stp...mais pas la réponse car je veux y ariver...

Merci beaucoup beaucoup :happy2: :happy2: :happy2:

par **Imod** » 11 Oct 2006, 13:58

Tu peux essayer de montrer que les deux vecteurs du "repère" sont orthogonaux .

Imod

par **fonfon** » 11 Oct 2006, 14:03

Salut,

Définition On appelle repère du plan, tout triplet ( O ;

,

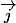
) où O est un point et

et

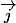
deux vecteurs non colinéaires. ...

Le point O est appelé origine du repère.
Les vecteurs i et j sont les vecteurs de base

par **nine** » 11 Oct 2006, 19:27

reuh :)

Donc si je prouve que I et J son non colinéaire ca peux marcher???

mais non... j'ai aucune valeur pour ca... :crash:

pfiou...merci mais je sais vraiment pas comment faire...je vais suremant passer cette question... :briques: :--:

merci de m'avoir dis toutes ces indications

:we: :we: :we: :we: :++: :++: :lol3:

ps : pourtant je suis pas de genre a baisser les bras :biere:

par **fonfon** » 12 Oct 2006, 08:45

Re,

reuh

Donc si je prouve que I et J son non colinéaire ca peux marcher???

mais non... j'ai aucune valeur pour ca...

et ça alors I=2i-2j et J=2i+2j tu peux en tirer quelques choses

par **nine** » 12 Oct 2006, 15:37

reuh :)
:id:
oui dsl...

ca fait donc :
I(2 ; -2)
J(2; 2)

(2*2)-(-2*2)= 8
donc ils ne sont pas colinaires

C'est ca??????? :happy2: :happy2: :we: :we:

par **Flodelarab** » 12 Oct 2006, 15:52

nine a écrit:reuh
:id:
oui dsl...

ca fait donc :
I(2 ; -2)
J(2; 2)

(2*2)-(-2*2)= 8
donc ils ne sont pas colinaires

C'est ca??????? :happy2: :happy2: :we: :we:

non!
Il faut prouver qu'il n'existe pas de k tel que

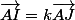
EDIT: tes coordonnée de I et J dans le vieux repère sont justes

par **Imod** » 12 Oct 2006, 17:25

Si nine connait le produit scalaire , l'exercice est résolu en deux secondes car I.J est clairement nul donc I et J orthogonaux donc indépendants .

Imod

par **Flodelarab** » 12 Oct 2006, 17:40

Imod a écrit:Si nine connait le produit scalaire , l'exercice est résolu en deux secondes car I.J est clairement nul donc I et J orthogonaux donc indépendants .

Imod

Ne crois tu qu'il faut un peu plus de 2 secondes ?
Car si

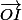
et

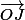
sont orthogonaux, cela ne prouve pas que

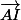
et

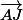
soient orthgonaux.

De plus, on a pas besoin d'avoir un repère orthogonal pour avoir un repère ...

Ceci dit ton raccourci est intéressant

par **Imod** » 12 Oct 2006, 17:50

Flodelarab a écrit:Ne crois tu qu'il faut un peu plus de 2 secondes ?
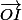
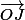
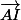
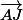
Car si et sont orthogonaux, cela ne prouve pas que et soient orthgonaux.

Je suis les notations de l'auteur , I et J sont des vecteurs et I=2i-2j et J=2i+2j donc I.J=(2i-2j)(2i+2j)=4i.i-4j.j=0 .

D'accord , disons dix secondes :we: et bien sûr cette méthode n'a rien de général car ici le repère a la gentillesse d'être orthogonal .

Imod

par **Flodelarab** » 12 Oct 2006, 17:52

:++:

ok g fait une faute lecture.

par **nine** » 14 Oct 2006, 10:06

reuh :)

euh...dsl mais je comprend pas...j'ai fait faux????

Repère

Repère

Qui est en ligne