messinmaisoui a écrit:Hello Boss_maths
Dans le 1) Si tu testes x = pi / 4 tu t'apercevras que ton système d'équations
n'est pas vérifié et puis il me semble que l'on cherche a et b pour que quelque soit x le système soit vérifié...
L'erreur à mon sens est ici : tu trouves (a-b ) * (sin x - cos x) = 0 ce qui est juste
mais tu as oublié de garder une des 2 équations initiales !
idem si a = b alors le système devient sin x + cos x = 1
ce qui n'est pas vérifié quelque soit x
Note : Pour moi il n'existe pas de relation entre a et b tel que ce système soit vérifié.
Qu'en penses tu ?
Je pense aussi, et la solution que je trouve à l'aide de la méthode matricielle :
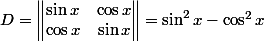
, puis
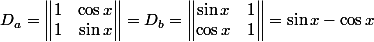
, soit :
=1)
et
=1)
. Finalement, par différence on obtient :

et
=-\cos(x))
Note pour le 2) je regarde maintenant ...
(\sin^2x+2\sin x\cos x+\cos^2x-3\sin x\cos x)=(\sin x+\cos x)\Big[(\sin x+\cos x)^2-3\Big(\dfrac{\sin 2x}{2}\Big)\Big])
Comme l'on a :
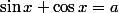
, je substitue dans la dernière expression et il vient :
=b\Leftrightarrow -3a\sin 2x=2(b-a^3)\Leftrightarrow \sin 2x=\dfrac{2(a^3-b)}{3a})
Mais, en tenant compte de la 1ère relation :
}{a})
on détermine, par différence, la relation entre

et

:
}{3a}-\dfrac{2(a-b)}{a}=0\Leftrightarrow \dfrac{2a^3-6a+4b}{3a}=0)
Merci bcp pour les réponses :lol3:
@+
