Regle sur les congruences

par **RomMac** » 17 Nov 2008, 20:18

Bonjours à tous,

j'ai entendus parlé d'une propriété de congruences et je voudrai savoir s'il elle existe vraiment ( car elle peut etre l'objet d'une erreur dans un DS de la part du prof ), la voici :

a congrus à b modulo( n), donc si p un nombre premier, alors p^a congrus a p^b modulo (n)

Merci d'avance

par **Luc** » 17 Nov 2008, 20:34

Salut,

C'est totalement faux :ptdr:

Essaye avec a=0 et b=n: ça te donne que pour tout nombre premier p,

(car

).

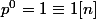
Un truc aussi général, si c'était vrai, ça ce saurait...
C'est faux pour p=2 et n=3, par exemple...
En effet

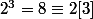
Luc

par **RomMac** » 17 Nov 2008, 20:51

Comment se fait-il alors que j'ai trouver tous les restes justes !?

par **leon1789** » 17 Nov 2008, 20:53

RomMac a écrit:Comment se fait-il alors que j'ai trouver tous les restes justes !?

fais voir tes calculs ?

par **Luc** » 17 Nov 2008, 20:53

Quel est l'énoncé de ton exercice?

par **Kah** » 17 Nov 2008, 20:56

Par contre, tu as bien:

Et la, si mes souvenirs sont bons, pas de conditions sur le "p".

par **leon1789** » 17 Nov 2008, 20:58

Kah a écrit:Par contre, tu as bien:

oula attention aux équivalences ! On a seulement l'implication

Kah a écrit:Et la, si mes souvenirs sont bons, pas de conditions sur le "p".

même sans modulo n, la réciproque est fausse (sur C par exemple) !

par **Luc** » 17 Nov 2008, 21:03

De façon plus générale, on a

et

impliquent

Luc

par **Kah** » 17 Nov 2008, 21:05

leon1789 a écrit:oula attention aux équivalences ! On a seulement l'implication

Ouaip trompé de signe désolé, je modifie mon post.

par **RomMac** » 17 Nov 2008, 21:12

Trouver les reste de la division euclidienne de 2^n par 7

par **Luc** » 17 Nov 2008, 21:18

Indice:

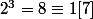
Pourquoi ceci nous permet de connaitre

pour tout n?

Regle sur les congruences

Regle sur les congruences

Qui est en ligne