2 réels t et u qui définissent des vecteurs
17 messages
- Page 1 sur 1
2 réels t et u qui définissent des vecteurs
Bonjour, je suis en terminale S et bloquée à la question 2 du DM que mon professeur m'a donné (sa commence TRES mal x( )
ABCDEFGH est un cube. Pour tout point I de la droite (AB) et tout point J de la droite (CG), on note M le centre de gravité du triangle EIJ.
On souhaite déterminer le lieu du point M lorsque les points I et J décrivent respectivement les droites (AB) et (CG)
On note [smb]epsilon[/smb] cet ensemble de point.
On se place dans le repère ( B, BC, BH, BA) de l'espace.
1/ Déterminer les coordonnées du centre de gravité Mo du triangle BEC
2/ Soit un point I sur la droite ( AB) et un point J sur la droite (CG)
a) Justifiez qu'il existe deux réels t et u tels que :
[smb]fleche[/smb] [smb]fleche[/smb] [smb]fleche[/smb] [smb]fleche[/smb]
BI = tBA CJ=uCG
b) En déduire les coordonnées des I et J en fonction de t et u.
Vérifier que les coordonnées du point M sont
(1/3;(u+1)/3;(t+1)/3)
et montrer que [smb]fleche[/smb] [smb]fleche[/smb] [smb]fleche[/smb]
MoM= (u/3)BF+(t/3)BA
c) En déduire que le point M appartient au plan P passant par Mo et dirigé par les vecteurs BF et BA
Pour la première j'ai trouvé pour B(0;0;0) C(1;0;0) et E(-1;1;0) (si vous pourriez me confirmer cette coordonnée sil vous plait ^^") et j'en ai déduit Mo(0;1/3;0)
Je crois pouvoir répondre seule aux autres questions mais en ce qui concerne les questions 2/b et 2/c je n'y arrive vraiment pas cela fait maintenant presque une semaine que je me penche dessus mais j'y arrive pas ^^"
je vous remercie d'avance de me sauver !! x)
ABCDEFGH est un cube. Pour tout point I de la droite (AB) et tout point J de la droite (CG), on note M le centre de gravité du triangle EIJ.
On souhaite déterminer le lieu du point M lorsque les points I et J décrivent respectivement les droites (AB) et (CG)
On note [smb]epsilon[/smb] cet ensemble de point.
On se place dans le repère ( B, BC, BH, BA) de l'espace.
1/ Déterminer les coordonnées du centre de gravité Mo du triangle BEC
2/ Soit un point I sur la droite ( AB) et un point J sur la droite (CG)
a) Justifiez qu'il existe deux réels t et u tels que :
[smb]fleche[/smb] [smb]fleche[/smb] [smb]fleche[/smb] [smb]fleche[/smb]
BI = tBA CJ=uCG
b) En déduire les coordonnées des I et J en fonction de t et u.
Vérifier que les coordonnées du point M sont
(1/3;(u+1)/3;(t+1)/3)
et montrer que [smb]fleche[/smb] [smb]fleche[/smb] [smb]fleche[/smb]
MoM= (u/3)BF+(t/3)BA
c) En déduire que le point M appartient au plan P passant par Mo et dirigé par les vecteurs BF et BA
Pour la première j'ai trouvé pour B(0;0;0) C(1;0;0) et E(-1;1;0) (si vous pourriez me confirmer cette coordonnée sil vous plait ^^") et j'en ai déduit Mo(0;1/3;0)
Je crois pouvoir répondre seule aux autres questions mais en ce qui concerne les questions 2/b et 2/c je n'y arrive vraiment pas cela fait maintenant presque une semaine que je me penche dessus mais j'y arrive pas ^^"
je vous remercie d'avance de me sauver !! x)
@mymi
Ce message [I]"montre" que ta réponse à la question 1) sur les coordonnées du point est correcte...
est correcte...
Donc ce message ne va pas t'aider à avancer dans ton exo
Désolé
[/I]
===================================
Bonjour
Il faut faire un dessin car c'est de la géométrie
(de plus il y a plusieurs possibilités pour placer les différents sommets d'un cube ABCDEFGH)
Voici l'image du cube ABCDEFGH pour que tu puisses le recopier sur ta feuille et placer les autres points.... :

Uploaded with ImageShack.us
On se place dans le repère ( B, BC, BH, BA) de l'espace
Dans ce repère
le point B a pour coordonnées ( 0 , 0 , 0 )
le point C a pour coordonnées ( 1 , 0 , 0 )
le point H a pour coordonnées ( 0 , 1 , 0 )
le point A a pour coordonnées ( 0 , 0 , 1 )
le point E a pour coordonnées (-1 , 1 , 0 ) (voir calculs *)
(Calculs *)

donc le vecteur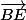 a pour coordonnées ( -1 , 1 , 0 ) dans la base (BC, BH, BA)
a pour coordonnées ( -1 , 1 , 0 ) dans la base (BC, BH, BA)
Pour information :
Si la longueur d'une arête du cube est 1 ( si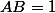 [I]par exemple ) alors
[I]par exemple ) alors  et
et  [/I]
[/I]
Soit le centre de gravité du triangle BEC
le centre de gravité du triangle BEC
donc est un isobarycentre
est un isobarycentre
c'est à dire le barycentre du système de points pondérés (B,
(B, ) , (E,
) , (E, ) , (C,
) , (C, )
) ) ou
ou  (B,1) , (E,1) , (C,1)
(B,1) , (E,1) , (C,1) )
Je vais prendre le point : barycentre du système
: barycentre du système  (B,1) , (E,1) , (C,1)
(B,1) , (E,1) , (C,1) )
D'après ton cours de maths sur les barycentres on a :
(cette relation vient de la [I]"vectorialisation" d'un barycentre )[/I]
Comme les coordonnées du vecteur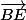 sont : ( -1 , 1 , 0 )
sont : ( -1 , 1 , 0 )
et que les coordonnées du vecteur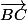 sont : ( 1 , 0 , 0 )
sont : ( 1 , 0 , 0 )
On en déduit que les coordonnées du vecteur sont : ( 0 ,
sont : ( 0 ,  , 0 ) dans la base (BC, BH, BA) de l'espace
, 0 ) dans la base (BC, BH, BA) de l'espace
CONCLUSION :
Le point a pour coordonnées : ( 0 ,
a pour coordonnées : ( 0 ,  , 0 ) dans le repère
, 0 ) dans le repère 
 ,
, 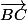 ,
, 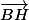 ,
, 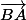
) de l'espace
de l'espace
ps)
J'ai écrit en rouge la correction de mon erreur signalée par un message de [I]chan
car en relisant cette discussion , j'ai vu que chan a effacé son message qui expliquait mon erreur
Pourquoi ? , donc j'ai corrigé
Merci à chan de re-re-lire (au cas où....)
A+[/I]
Ce message [I]"montre" que ta réponse à la question 1) sur les coordonnées du point
Donc ce message ne va pas t'aider à avancer dans ton exo
Désolé
[/I]
===================================
Bonjour
Il faut faire un dessin car c'est de la géométrie
(de plus il y a plusieurs possibilités pour placer les différents sommets d'un cube ABCDEFGH)
Voici l'image du cube ABCDEFGH pour que tu puisses le recopier sur ta feuille et placer les autres points.... :

Uploaded with ImageShack.us
On se place dans le repère ( B, BC, BH, BA) de l'espace
Dans ce repère
le point B a pour coordonnées ( 0 , 0 , 0 )
le point C a pour coordonnées ( 1 , 0 , 0 )
le point H a pour coordonnées ( 0 , 1 , 0 )
le point A a pour coordonnées ( 0 , 0 , 1 )
le point E a pour coordonnées (-1 , 1 , 0 ) (voir calculs *)
(Calculs *)
donc le vecteur
Pour information :
Si la longueur d'une arête du cube est 1 ( si
Soit
donc
c'est à dire le barycentre du système de points pondérés
Je vais prendre le point
D'après ton cours de maths sur les barycentres on a :
(cette relation vient de la [I]"vectorialisation" d'un barycentre )[/I]
Comme les coordonnées du vecteur
et que les coordonnées du vecteur
On en déduit que les coordonnées du vecteur
CONCLUSION :
Le point
ps)
J'ai écrit en rouge la correction de mon erreur signalée par un message de [I]chan
car en relisant cette discussion , j'ai vu que chan a effacé son message qui expliquait mon erreur
Pourquoi ? , donc j'ai corrigé
Merci à chan de re-re-lire (au cas où....)
A+[/I]
@chan79
Merci pour avoir "réparé" mes "conneries"
A ne pas faire des calculs , voila le genre [I]"d'annerie" qu'on arrive à écrire.....[/I]
EDIT
@chan79
Vu que tu as supprimé ta correction (pourquoi ?), j'ai corrigé mon message précédent.
Merci de le re-re-lire et de re-rectifier s'il y a encore une erreur...
A +
Merci pour avoir "réparé" mes "conneries"
A ne pas faire des calculs , voila le genre [I]"d'annerie" qu'on arrive à écrire.....[/I]
EDIT
@chan79
Vu que tu as supprimé ta correction (pourquoi ?), j'ai corrigé mon message précédent.
Merci de le re-re-lire et de re-rectifier s'il y a encore une erreur...
A +
ptitnoir a écrit:@chan79
Merci pour avoir "réparé" mes "conneries"
A ne pas faire des calculs , voila le genre [I]"d'annerie" qu'on arrive à écrire.....[/I]
EDIT
@chan79
Vu que tu as supprimé ta correction (pourquoi ?), j'ai corrigé mon message précédent.
Merci de le re-re-lire et de re-rectifier s'il y a encore une erreur...
A +
alors
E(-1,1,0)
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
