Récurrence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Juin 2010, 15:57
par girdav » 30 Juin 2010, 15:57
froudjik a écrit:Et une autre question dans la continuité du second exo. Comment faire pour prouver que
x^n+nx^{n+1}}{(1-x)^2}\| \leq \frac{1-(n+1)|x|^n+n|x|^{n+1}}{(1-|x|)^2})
?
Applique l'inégalité triangulaire à la somme d'origine.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Juin 2010, 16:14
par benekire2 » 30 Juin 2010, 16:14
Tient, je me rapelle de ton thread, et je voulais savoir, pour la première ligne de la première méthode, tu as justé développé et réécrit avec tes sommes sym ?
Normalement c'est ça ... mais c'est juste que c'est extrêmement long ....

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Juin 2010, 16:16
par Olympus » 30 Juin 2010, 16:16
benekire2 a écrit:Tient, je me rapelle de ton thread, et je voulais savoir, pour la première ligne de la première méthode, tu as justé développé et réécrit avec tes sommes sym ?
Euh... Ouép ^^
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Juin 2010, 16:27
par benekire2 » 30 Juin 2010, 16:27
Ok, je me disais bien ... :we:
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 30 Juin 2010, 17:19
par froudjik » 30 Juin 2010, 17:19
Olympus a écrit:Ben, la démo étant très facile, je te la laisse . C'est en fait la même astuce que dans le lien que je t'ai donné ^^
Par contre, petite correction de ton inégalité, c'est plutôt :
 ^2)
.
Heu mais je comprends pas pourquoi c'est pas
 ^2)
Je me trompe peut-être (sûrement), mais d'après ce que je comprends, pour
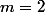
, avec ta formule on aurait
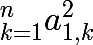\(\bigsum_{k=1}^n a_{2,k}^2\) \geq \(\bigsum_{k=1}^n (a_{k,1}+a_{k,2})\)^2)
et non
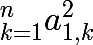\(\bigsum_{k=1}^n a_{2,k}^2\) \geq \(\bigsum_{k=1}^n a_{k,1}a_{k,2}\)^2)
Bon, j'ai sûrement rien compris, mais j'attends que tu m'expliques ^^

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Juin 2010, 17:24
par Olympus » 30 Juin 2010, 17:24
Oula, la deuxième c'est un grand Pi pas une sigma, pas vu je corrige .
EDIT : voilà c'est corrigé, en fait, dans ton inégalité, t'avais inversé m et n, c'est pour ça que j'ai dit que c'était faux .
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 30 Juin 2010, 17:31
par froudjik » 30 Juin 2010, 17:31
Ah ok merci j'avais pas vu :dodo:
Et j'ai compris pour la démonstration grâce à ton lien.
Par contre je comprends pas ce que veut dire le symbole

?

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Juin 2010, 17:40
par Olympus » 30 Juin 2010, 17:40
@froudjik : la somme sur toutes les n! permutations des n variables .
Donc par exemple pour 3 variables :
 = f \left( x;y;z \right) + f\left(y;x;z\right) + f\left( y;z;x \right) + f\left( z;y;x \right) + f\left( z;x;y \right) + f\left( x;z;y \right))
.
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 30 Juin 2010, 22:00
par froudjik » 30 Juin 2010, 22:00
Merci, c'est bizarre je n'avais jamais vu ce symbole auparavant...
girdav a écrit:Applique l'inégalité triangulaire à la somme d'origine.
Je pense avoir trouvé une solution valable, dites moi si c'est bon :
Soient

et

Montrons que
| \leq f(|x|))
avec
=\frac{1-(n+1)x^n+nx^{n+1}}{(1-x)^2})
=\frac{1-(n+1)x^n+nx^{n+1}}{(1-x)^2}=\frac{(1-x^n)+(nx^{n+1}-nx^n)}{(1-x)^2}=\frac{(1-x)\bigsum_{i=0}^{n-1}x^i-nx^n(1-x)}{(1-x)^2}\\=\frac{\bigsum_{i=0}^{n-1}x^i-nx^n}{1-x}=\frac{\bigsum_{i=0}^{n-1}(x^i-x^n)}{1-x}=\frac{\bigsum_{i=0}^{n-1}x^i(1-x^{n-i})}{1-x}=\frac{\bigsum_{i=0}^{n-1}x^i(1-x)\bigsum_{j=0}^{n-i}x^j}{1-x}\\=\Bigsum_{i=0}^{n-1}x^i\Bigsum_{j=0}^{n-i}x^j=P(x))
ou
)
est un polynôme en

.
Ainsi, on applique l'inégalité triangulaire :
|=|P(x)|\leq P(|x|)=f(|x|))
Un peu facile mais bon je vois rien d'autre...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 30 Juin 2010, 22:08
par girdav » 30 Juin 2010, 22:08
Attention, l'inégalité
 |\leq P\(|x|))
est fausse en général (par exemple
= X-1)
et
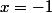
mais elle est vraie si les coefficients sont positifs, ce qui est le cas ici.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Juin 2010, 22:23
par Olympus » 30 Juin 2010, 22:23
froudjik a écrit:Merci, c'est bizarre je n'avais jamais vu ce symbole auparavant...
Normal, il est utilisé uniquement dans le monde des olympiades ^^
Il y a aussi une notation plus académique, dont je me souviens plus, mais qui fait apparaître des petits sigmas (

) aux indices de la somme .
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 01 Juil 2010, 15:44
par froudjik » 01 Juil 2010, 15:44
Ah d'accord je me disais bien :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
?
.