Récurrence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 28 Juin 2010, 16:58
par Olympus » 28 Juin 2010, 16:58
Et pour ta culture personnelle, avec le résultat de ton exercice en début du sujet, tu peux très aisément prouver l'inégalité suivante ( je pense même que c'est le but de l'exercice ) :
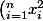 \left( \bigsum_{i=1}^n y^2_i \right) \geq \left( \bigsum_{i=1}^n x_i y_i \right)^2)
.
Et c'est l'inégalité de Cauchy-Schwarz

-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 28 Juin 2010, 17:54
par froudjik » 28 Juin 2010, 17:54
Ben ca découle tout seul du fait que
^2)
est positif non ?
En tout cas super ce forum, je commence vraiment à bien aimer les maths, et je pense que ca pourra bien m'aider à progresser.
Merci à vous


-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 28 Juin 2010, 18:01
par Olympus » 28 Juin 2010, 18:01
froudjik a écrit:Ben ca découle tout seul du fait que
^2)
est positif non ?
Voilà

En tout cas super ce forum, je commence vraiment à bien aimer les maths, et je pense que ca pourra bien m'aider à progresser.
Merci à vous

No soucis

-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 28 Juin 2010, 22:21
par benekire2 » 28 Juin 2010, 22:21
ca ne pourrait pas te faire régresser c'est sûr :happy3: !!
Faut pas oublier que les maths c'est pas que pour les "doués" et que ça peut être pour tout le monde ( bibi :) ) , sous plusieurs formes.
Soit le bienvenu :id:
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 29 Juin 2010, 16:19
par froudjik » 29 Juin 2010, 16:19
Rebonjour

J'ai un autre petit problème pour une égalité.
Je n'arrive pas à prouver par récurrence que :
x^{n+1}+nx^{n+2}}{(1-x)^2})
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 29 Juin 2010, 16:31
par girdav » 29 Juin 2010, 16:31
Je suppose que c'est l'hérédité qui te pose problème.
Je n'ai pas fait les calculs mais il y a fort à parier qu'il faille réduire au même dénominateur puis "charcuter" le numérateur : développer puis ordonner.
On peut obtenir la formule directement :
' =x\(\bigsum_{k=1}^nx^k\)')
et la somme dans le "prime" est plus facile à calculer.
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 29 Juin 2010, 17:16
par froudjik » 29 Juin 2010, 17:16
erreur, à supprimer...
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 29 Juin 2010, 17:28
par froudjik » 29 Juin 2010, 17:28
J'arrive à un résultat totalement absurde, je vois pas ou sont les erreurs...
x^n)(1-x)+x-x^{n+1}}{(1-x)^2}\\\Longleftrightarrow\bigsum_{k=1}^{n}kx^{k-1}=\frac{1-x-nx^n-x^n+nx+x+x-x^{n+1}}{(1-x)^2}\\\Longleftrightarrow\bigsum_{k=1}^{n}kx^{k-1}=\frac{1-(n+1)(x^n+x)-x^{n+1}}{(1-x)^2}\\\Longleftrightarrow\bigsum_{k=1}^{n}kx^{k}=\frac{x-(n+1)(x^{n+1}+x^2)-x^{n+2}}{(1-x)^2})
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 29 Juin 2010, 17:45
par benekire2 » 29 Juin 2010, 17:45
Salut ,
Tu n'as pas l'air de raisonner par récurrence ici ... puisque par récurrence c'est quand même assez facile. Le mieux ici c'est la solution de girdav :id:
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 29 Juin 2010, 18:01
par froudjik » 29 Juin 2010, 18:01
Justement ici je fais la solution de girdav, j'ai dérivé
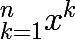
puis multiplié par

.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 29 Juin 2010, 18:14
par girdav » 29 Juin 2010, 18:14
Pour cette somme là il n'y en a pas besoin : ce sont les termes d'une suite géométrique. Tu peux calculer
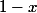
fois cette somme pour la simplifier.
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 29 Juin 2010, 18:19
par froudjik » 29 Juin 2010, 18:19
froudjik a écrit:J'arrive à un résultat totalement absurde, je vois pas ou sont les erreurs...
x^n)(1-x)+x-x^{n+1}}{(1-x)^2}\\\Longleftrightarrow\bigsum_{k=1}^{n}kx^{k-1}=\frac{1-x-nx^n-x^n+nx+x+x-x^{n+1}}{(1-x)^2}\\\Longleftrightarrow\bigsum_{k=1}^{n}kx^{k-1}=\frac{1-(n+1)(x^n+x)-x^{n+1}}{(1-x)^2}\\\Longleftrightarrow\bigsum_{k=1}^{n}kx^{k}=\frac{x-(n+1)(x^{n+1}+x^2)-x^{n+2}}{(1-x)^2})
C'est ce que j'ai fait il me semble. Il doit y avoir une erreur de calcul, j'ai beau regarder mais je ne vois pas où...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 29 Juin 2010, 18:23
par girdav » 29 Juin 2010, 18:23
La formule de la première ligne ne va pas : c'est
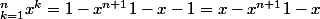
pour
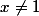
.
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 29 Juin 2010, 18:24
par froudjik » 29 Juin 2010, 18:24
C'était une faute de frappe, j'ai modifié...
De la ligne 1 à la ligne 2 j'ai dérivé, et de la 4 à la 5 j'ai multiplié par

. Le reste j'ai développé, factorisé... et je comprends pas comment on peut en arriver là.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 29 Juin 2010, 19:02
par girdav » 29 Juin 2010, 19:02
On a
x^n\)\(1-x\) +x-x^{n+1} = 1-x+\(x-1\)\(n+1\)x^n+x+x^{n+1}=1+\(n+1\)x^{n+1}-\(n+1\)x^n-x^{n+1})
et tu peux conclure.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 29 Juin 2010, 19:14
par Olympus » 29 Juin 2010, 19:14
T'as fait une erreur lors de la factorisation après avoir développé .
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 29 Juin 2010, 23:36
par froudjik » 29 Juin 2010, 23:36
Effectivement, j'ai compris mon erreur, et retrouvé le résultat correct, merci à vous.
Sinon pour revenir sur l'inegalité de Cauchy-Schwarz, j'ai une question.
Peut-on la généraliser ? Genre
^2)
?
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 30 Juin 2010, 11:25
par froudjik » 30 Juin 2010, 11:25
Et une autre question dans la continuité du second exo. Comment faire pour prouver que
x^n+nx^{n+1}}{(1-x)^2}\| \leq \frac{1-(n+1)|x|^n+n|x|^{n+1}}{(1-|x|)^2})
?

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Juin 2010, 13:45
par Olympus » 30 Juin 2010, 13:45
froudjik a écrit:Effectivement, j'ai compris mon erreur, et retrouvé le résultat correct, merci à vous.
Sinon pour revenir sur l'inegalité de Cauchy-Schwarz, j'ai une question.
Peut-on la généraliser ? Genre
^2)
?
Ouép, m'enfin, je crois avoir déjà démontré Cauchy-Schwarz à trois produits ( ici :
http://maths-forum.com/showthread.php?t=102720 , partie "Deuxième preuve" ) , donc cela marchera sûrement avec n produits .
Je regarde vite fait pour une "généralisation" et je te répondrai .
Mais on peut pas vraiment parler de généralisation car par exemple une Cauchy-Schwarz-like à 3 produits est moins forte qu'une Cauchy-Schwarz à 2 produits .

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Juin 2010, 14:26
par Olympus » 30 Juin 2010, 14:26
Ben, la démo étant très facile, je te la laisse . C'est en fait la même astuce que dans le lien que je t'ai donné ^^
Par contre, petite correction de ton inégalité, c'est plutôt :
 ^2)
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
' =x\(\bigsum_{k=1}^nx^k\)') et la somme dans le "prime" est plus facile à calculer.
et la somme dans le "prime" est plus facile à calculer.?
