Récurrence Suites

[Radougl]

Donc, on suppose que la proposition est vraie. Prenons k

car, précédemment
C'est donc une suite croissante.

[Teacher]

Non c'est horrible !
Prouver par récurrence que pour tout :

Initialisation pour le premier rang (n=0):

D'après l'énoncé: donc .

La propriété est donc vraie au rang n=0.

Jusque là tout va bien ! Maintenant:

Hérédité:

Supposons que la propriété est vraie au rang k, c'est à dire : .... ?
Montrons qu'elle est vraie au rang k+1, c'est à dire: .... ?

[Radougl]

Soit ?

[Teacher]

Non c'est pour le rang k+1 ce que tu écris là !
On suppose pour le rang k puis on démontre ce que tu viens d'écrire soit que c'est vraie au rang k+1.
Avec les 2 gros postes du dessus en relisant tu devrais pouvoir trouver les ....

[Radougl]

Ou sa ne donne pas quelque chose comme cela?
Fixons k, on suppose que
est croissante donc,
Donc,
Elle est donc vérifiée au rang k+1.

[Teacher]

T'es sur un autre forum et tu es en train de gober tout ce que l'on t'y racompte ?
Ou tu recopies un ancien poste ?

[Radougl]

Non pas du tout j'ai utilisé une méthode de résolution pour trouver ce que je venais d'écrire.

[Radougl]

J'ai trouvé une méthode et tenté de l'appliquer dans ce cas présent, sur un exercice ou la suite était majorée donc sa avait l'air de concorder avec cet exercice..

[Teacher]

Hérédité:

Supposons que la propriété est vraie au rang k, c'est à dire : .... ?
Montrons qu'elle est vraie au rang k+1, c'est à dire prouver que: .... ?

[Radougl]

C'est a dire prouver que la propriété est vrai pour k fixé dans
Et au rang k+1 c'est prouver que elle est vérifiée quelque soit k.

[Teacher]

Non !
On la suppose vraie au rang k donc on ne la démontre pas au rang k mais au rang k+1 !
Mais avec la propriété écrite (avec U_k+1) ça revient à démontrer quoi ?

[Radougl]

C'est prouver que 01

[Teacher]

Je pense que tu n'as pas très bien compris le principe de la récurrence.
Prenons un escalier avec n la n-iéme marche de l'escalier.
Le principe de récurrence dit que:

Initialisation
Si l'on sait monter la toute première marche, ( A tester = Initialisation )
Hérédité
Puis si on suppose que l'on sait monter sur la marche d'après, (A écrire = Hypothèse )
Puis si on arrive à prouver que sur la marche d'après on arrive toujours à monter une marche. (A démontrer)
Conclusion
Alors: on arrive à monter toutes les marches.

[Teacher]

Démontre pour commencer que:

[Radougl]

Donc, il faut démontrer que,
01
soit, 01
C'est exact?

[Teacher]

Non !
Démontre pour commencer que:

[Radougl]

Avec votre formule j'y arrive mais avec la formule de départ je n'y arrive pas.

[Teacher]

Oui avec ma formule !

[Radougl]

Hé bien j'y arrive avec la formule mais après je ne vois pas comment continuer...

[Teacher]

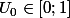
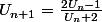
On sait que et ou
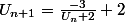
A savoir dans une récurrence il faut toujours utilisé l'hypothèse écrite, noté (H.R.)

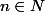
Prouver par récurrence que pour tout on a :

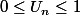
Initialisation pour le premier rang (n=0):

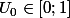
D'après l'énoncé: donc .

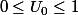
La propriété est donc vraie au rang n=0.

Jusque là tout va bien ! Maintenant:

Hérédité:

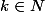
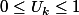
Supposons que la propriété est vraie au rang k, avec , c'est à dire : vraie (H.R.)
Montrons qu'elle est vraie au rang k+1, c'est à dire: .
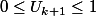
Montrons qu'elle est vraie au rang k+1, c'est aussi montrer que: .

D'après l'hypothèse de récurrence(c'est là qu'on utilise l'H.R.):
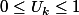
Maintenant à partir de l'H.R. il faut montrer que .
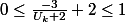