Recherche exercices arithmétique

[zygomatique]

Je regarderai alors ! :lol3:
Merci !
Juste une question: les entiers sont-ils tous positifs ou ils sont juste non nuls ? :hein:

a est positif signifie

a est négatif signifie

0 est le seul nombre positif et négatif, c'est pourquoi il est nul ....

:lol3:


entiers (naturels) :: 0, 1, 2, ....

entiers relatifs : entiers ou opposé d'un entier

....

[Mikihisa]

En fait il manque une condition pas évidente du tout :p je pensais que tu y serait arrive :

Donc on a remarquer que doit être premier avec et car sinon on pourrais factoriser le numérateur et le dénominateur par p divisant . Et de même pour .

On sa supposer que ces conditions sont vérifié.
On suppose qu'il existe n tel que F(n) soit réductible.
Donc il existe p premier tel que
Et

Si p divise , alors p divise - et donc p divise
Lemme d'Euclide : p divise ou p divise ( car p divise mu.beta car p est premier). Et c'est impossible car p divise et sont premier entre eux. (Supposition du départ).
Donc p ne divise pas et on montre de la même manière que p ne divise pas non plus .
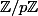
Donc les classes de sont non-nuls dans le corps alors on peut diviser les deux congruence. ( et oui, si il faut que p soit premier il faut également que les nombre ne soit pas congru a 0 modulo p, car on ne peux pas diviser par 0, tout ça juste pour montrer qu'ils ne sont pas congru 0 et qu'ont peut bien diviser ^^)

Donc en divisant les 2 première congruence ont obtient en effet
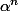
Puis en divisant la premier congruence par ( comme alpha et beta sont congru) on obtient .


Voilà donc on arrive a la même conclusion, dans ton raisonnement il faut juste montrer que p ne divise pas alpha, beta, lambda et mu pour t'assurer que tu peux bien diviser tes congruences.

Mais en fait on a prouver quoi ?? On a prouvé :

C'est a dire :


Et donc par contraposé on déduit la condition suivante pour que F(n) soit irréductible : en plus de la condition de départ.

Il reste a s'assurer que ces deux conditions suffisent ( en raisonnant par l'absurde). C'est déjà tout fais en soi.


Ps : pas compris pourquoi tu viens nous invoquer Bezout et ses identités. Tu veux montrer

Raisonne par contraposé !! Si pgcd(alpha,beta)>1 ou pgcd(...)>1 ou ... Alors on peut factoriser et F(n) est réductible en fait c'est exactement ce qu'on a prouver au tout début de l'exercice : dans mon tout premier indice, et dans les première lignes de ce message. Lors d'un examen perdre du temps a faire compliquer sur une question simple, c'est du temps de perdu pour réfléchir sur les question compliquer

[zygomatique]

donc



donc a, b, u et v doivent être premiers entre eux deux à deux ... mais est-ce suffisant ?

[Mikihisa]

Est-ce suffisant ? C'est ce qu'on essai de prouver en fait :p

Et en réalité ! Non ce n'est pas suffisant, il faut de plus que pgcd(a-b,u+v)=1. Je te renvois a mon message précédent.

[Waax22951]

En fait il manque une condition pas évidente du tout :p je pensais que tu y serait arrive :

Donc on a remarquer que doit être premier avec et car sinon on pourrais factoriser le numérateur et le dénominateur par p divisant . Et de même pour .

On sa supposer que ces conditions sont vérifié.
On suppose qu'il existe n tel que F(n) soit réductible.
Donc il existe p premier tel que
Et

Si p divise , alors p divise - et donc p divise
Lemme d'Euclide : p divise ou p divise ( car p divise mu.beta car p est premier). Et c'est impossible car p divise et sont premier entre eux. (Supposition du départ).
Donc p ne divise pas et on montre de la même manière que p ne divise pas non plus .
Donc les classes de sont non-nuls dans le corps alors on peut diviser les deux congruence. ( et oui, si il faut que p soit premier il faut également que les nombre ne soit pas congru a 0 modulo p, car on ne peux pas diviser par 0, tout ça juste pour montrer qu'ils ne sont pas congru 0 et qu'ont peut bien diviser ^^)

Donc en divisant les 2 première congruence ont obtient en effet
Puis en divisant la premier congruence par ( comme alpha et beta sont congru) on obtient .


Voilà donc on arrive a la même conclusion, dans ton raisonnement il faut juste montrer que p ne divise pas alpha, beta, lambda et mu pour t'assurer que tu peux bien diviser tes congruences.

Mais en fait on a prouver quoi ?? On a prouvé :

C'est a dire :


Et donc par contraposé on déduit la condition suivante pour que F(n) soit irréductible : en plus de la condition de départ.

Il reste a s'assurer que ces deux conditions suffisent ( en raisonnant par l'absurde). C'est déjà tout fais en soi.


Ps : pas compris pourquoi tu viens nous invoquer Bezout et ses identités. Tu veux montrer

Raisonne par contraposé !! Si pgcd(alpha,beta)>1 ou pgcd(...)>1 ou ... Alors on peut factoriser et F(n) est réductible en fait c'est exactement ce qu'on a prouver au tout début de l'exercice : dans mon tout premier indice, et dans les première lignes de ce message. Lors d'un examen perdre du temps a faire compliquer sur une question simple, c'est du temps de perdu pour réfléchir sur les question compliquer

En même temps si on me cache des choses..! :p
En réalité j'ai réfléchis en me disant que la propriété était suffisante sans me demander si c'était vraiment le cas..!
Du coup j'ai presque tout essayé pour trouver une preuve absurde mais je n'ai pas trouvé (et je comprends pourquoi maintenant..).
Pour la division par zéro, je n'y avais pas pensé, c'est vrai, ça me servira de leçon ! :lol3:
J'ai juste une question qui est plus d'ordre général plutôt que dans l'exercice même. Tu déduis par contraposée que le fait que F(n) soit irréductible implique que le PGCD soit égal à 1, mais comment le déduire en général ?
Est-ce toujours vrai ou faut-il faire au cas par cas ?
En effet.. En réalité j'ai utiliser la première méthode qui me soit venue à l'esprit, voilà tout :lol3:
Je vais réfléchir à la preuve pour la suffisance, mais je ne sais pas si je vais pouvoir le finir ce soir :lol3:
Bonne soirée !

PS: En fait non je crois avoir trouvé, du coup je met la preuve et comme ça vous pourrez me dire plus vite si c'est bon ^^"
(J'ai pas mal de choses sur le feu donc si je ne le fais pas ce soir ça sera pas avant jeudi soir et encore je ne suis pas sûr.. Donc je préfère l'envoyer plus tôt plutôt que plus tard :lol3: )

On pose, pour tout entiers , , et , la propriété définie par:
.
On pose aussi la fraction . On pose la propriété suivante: est irréductible.

On a déjà démontré que pour tout n, .
Démontrons maintenant que .
Supposons qu'il existe de tels entiers vérifiant mais pas .
Cela signifie que pour un rang n, est réductible, donc il existe un nombre premier p qui divise son dénominateur et son numérateur. Autrement dit:
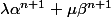
p divise à la fois et .
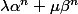
On a donc:
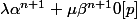
et .
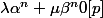
D'où et .

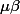
Si p divise , alors il divise , donc il divise . S'il divise , il divise aussi , puisqu'il est premier. Le lemme d'Euclide affirme qui si p divise divise , alors ou . Ceci est absurde puisque p divise et que est premier avec et .
On démontre de manière analogue que p ne divise pas , , et , donc leurs classes sont non-nulles dans le corps .
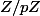
De plus, divise et divise .
Puisque p est premier, on a:
.

On a donc aussi , d'où
.
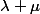
Donc p divise , il divise donc ou (Lemme d'Euclide).

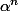
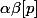
Si p divise , alors p divise . Or donc il divise aussi , ce qui est absurde puisque et sont premiers entre eux. Donc p divise .

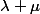
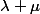
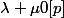
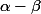
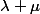
Si p divise , alors , or . Donc . Donc p divise à la fois et , ce qui est absurde puisqu'ils sont premiers entre eux.

Il n'existe donc pas un tel p. Donc est irréductible.

On a donc bien .
Donc finalement, on a .

Voilà voilà.. J'espère que c'est bon cette fois ci

PPS: Au sujet des exercices, je pense que ce sera le dernier que je fais avec vous ! ( )
(Je reviens le 11 août, autrement dit dans longtemps )
Cependant, si vous pouviez me trouver un petit exercice un peu plus simple que je puisse faire sans l'aide de personne, ce serait vraiment génial de votre part !
Merci pour tout et bonne continuation sur la forum ! :lol3:

[Mikihisa]

Ça tombe bien c'était le dernier que j'avais a te proposer ^^

Bonne vacance ! Acheté toi un bouquin :)
Si tu habite près de paris : gibert Joseph boulevard st Michel au dernier étage :p

[paquito]

Si tu veux un exercice raisonnable mais intéressant, tu as celui ci:

déterminer tous les triplets (a,b,c) d'entiers naturels non nuls tels que:

,
puis montrer que pour tout triplet solution il existe un entier d tel que

(quadruplets pythagoriques).

[Waax22951]

Ça tombe bien c'était le dernier que j'avais a te proposer ^^

Bonne vacance ! Acheté toi un bouquin
Si tu habite près de paris : gibert Joseph boulevard st Michel au dernier étage :p

Ça tombe bien alors ! :lol3:
Je pense que c'est ce que je vais faire mais je le trouverai plus simplement sur internet vu ma situation géographique.. :lol3:
Si un jour je passe par Paris je penserai à cette adresse (au pire je demanderai à mon frère qui y va plus souvent..)
Merci, bonne continuation ! :lol3:

Si tu veux un exercice raisonnable mais intéressant, tu as celui ci:

déterminer tous les triplets (a,b,c) d'entiers naturels non nuls tels que:

,
puis montrer que pour tout triplet solution il existe un entier d tel que

(quadruplets pythagoriques).

Ah..! Je vais finir par haïr ces équations ! :lol3:
Merci, je pense qu'il va bien m'occuper le temps du trajet, ça me permettra de m'entraîner sur ce dont j'ai le plus le mal ! :lol3:
Bonne continuation à tous ! :we:

[Waax22951]

Si je n'ai pas fait d'erreur (dans un bus c'est pas facile de se concentrer..), l'ensemble des solutions S est avec .
De ce fait la valeur de d est 3n.
Ce qui me dérange c'est que a et b sont égaux, mais j'ai démontré qu'ils ne peuvent pas être distincts.. Du coup je me demande si j'ai pas fait une erreur de logique
Bonne journée !

[paquito]

Bonjour Waax,

en fait tu as traité un cas particulier, mais il y a bien d'autres solutions: a=4 et b=12, ou a = 6 et b=30; en fait tu as traité le cas a=b; pourquoi dans une étape suivante, ne pas envisager a=kb, avec k entier, tu vas trouver bien d'autres solutions; pour trouver tous les solutions ensuite, il y a une astuce qui n'est évidente et je te mettrais sur la voie.

Bonnes vacances.

[Waax22951]

Bonjour Waax,

en fait tu as traité un cas particulier, mais il y a bien d'autres solutions: a=4 et b=12, ou a = 6 et b=30; en fait tu as traité le cas a=b; pourquoi dans une étape suivante, ne pas envisager a=kb, avec k entier, tu vas trouver bien d'autres solutions; pour trouver tous les solutions ensuite, il y a une astuce qui n'est évidente et je te mettrais sur la voie.

Bonnes vacances.

J'ai du faire une erreur dans mon raisonnement, car j'en ai déduit que a et b sont forcément égaux..!
Je vais mettre ma démarche pour qu'on puisse y voir plus clair.. Mais je préviens tout de suite: je ne peux qu'écrire sur mon portable, donc pas de Latex, désolé !

Remarque préliminaire: Soit a b et n trois entiers naturels non nuls. Si n divise a+b et a, alors n divise b.
En effet, on peut écrire a+b=pn et a=qn avec p et q deux entiers naturels non nuls tels que p>q
On a donc a+b=pn b=pn-qn b=n(p-q).
(p-q) est un entier naturel strictement positifs donc b est un multiple de n (donc n divise b).

On pose (E) l'équation suivante:
(E): 1/a+1/b=1/c
Avec a b et c trois entiers naturels non nuls.
Si a=b, alors on a c=a/2.
c est entier si et seulement si a est pair, donc l'ensemble des solutions lorsque a=b est S=(2n, 2n, n).

Si a=c ou b=c, alors 1/b=0 ou 1/a=0, donc 1=0, ce qui est absurde donc a et b sont distincts de c.

Supposons maintenant que a b et c sont distincts. On pose 1/ab>c.
On remarque que:
(E): 1/a+1/b=1/c (E'): ac+bc=ab.
Donc a et b divisent ac+bc. Or a divise ac et b divise bc, donc a divise bc et b divise ac.
Or a est supérieur à b et à c, donc a ne divise ni a ni c. Donc a ne divise pas bc, ce qui est absurde.
Donc a b et c ne peuvent pas être distincts.
L'unique ensemble de solutions est, pour tout n non nul:
S=(2n, 2n, n).

Bon.. Du coup je vais réfléchir à une autre alternative..!

Par contre je préfère trouver la solution seul et sans indices, je pense que cet comme ça que j'avancerai !

PS: c'est bon en fait j'ai réalisé mon erreur.. En réalité la dernière remarque n'est vraie que si a est premier..!
(Je profite d'une escale à Marseille mais je n'ai pas internet de temps normal.. Mais je réfléchis quand même au problème ! )


PPS: Du coup en gribouillant de temps en temps, j'ai réussi à montrer que l'ensemble des solutions est l'ensemble des triplets d'entiers strictement positifs a et b tels que:

Il suffit donc de trouver l'ensemble des couples (a; b) tels que a+b divise ab.
On montre aussi que a et b ne sont pas premiers entre eux.
Après je n'ai pas pu me concentrer donc je n'ai pas non plus trop avancé..!
J'ai aussi pu obtenir l'ensemble des solutions en dessous d'un certain seuil, mais ça ne m'a pas beaucoup servi..!
(Mis à part le fait que b ne divise pas tout le temps a..)

[paquito]

Je t'ai donné comme solution: 1/a=1/12,1/ b=1/4 et 1/c=1/3; on a bien 1/a<1/b<1/c et a, b et c sont solutions, donc ce n'est pas la peine de chercher à démontrer que 1/a<1/b<1/c est impossible;

sans te donner de directive, je te montre un cas particulier: y a t'il des solution avec a=2b?

1/a+1/b=(a+b)/ab=3b/2b²=3/2b; comme 2 ne divise pas 3, b doit être de la forme 3k, k entier strictement positif, ce qui donne a=6k,b=3k et c=2k (vérification 1/6k+1/3k=(1+2)/6k=1/2k); j'ai donc trouver une infinité de solutions (ne t'inquiète pas, il en reste);

De plus (6k)²+(3k)²+(2k)²=49k²=(7k)².

Essaie de commencer par des choses simples et à avancer progressivement; la solution ne se trouve pas du premier coup.

[Waax22951]

Home, Sweet Home !
Je suis rentré il y un jour donc j'ai pu revoir un peu mes calculs en les posant !
Merci pour ces conseils, ils l'ont bien aidé
Donc j'ai bien réussi pour les cas où b divisent a et j'ai aussi montré que a et b ne sont pas premiers (donc que a n'est pas premier).

Considérons les cas où b divise a. Il existe donc un entier naturel non nul q tel que a=bq

On a alors:


Puisque c est un entier, q+1 divise bq.
Puisque q+1 divise bq, tous les facteurs premiers de q+1 apparaissent dans bq. Or PGCD(q+1; q)=1 (propriété de deux nombres consécutifs), donc aucun facteur premier de q+1 apparaît dans q, donc tous les facteurs premiers de q+1 apparaissent dans b, donc q+1 divise b.
Il existe donc un entier p tel que:
b=(q+1)p.
On en déduit que a=pq(q+1).

En remplaçant a et b par leur valeurs, on obtient c=pq. Puisque c est un entier naturel non nul pour tout p et q, on en déduit qu'il existe des solutions pour toutes les valeurs de p et de q.

Donc, pour tout entiers non nuls p et q, le tripler (pq(q+1); p(q+1); pq) est solution de (E).

On remarque aussi que:
donc il existe un d tel que et

J'ai aussi remarqué qu'il y avait des solutions où b ne divisait pas a, donc j'essaie de nouveau de généraliser mon résultat pour tout a et b non premiers entre eux (puisqu'ils ne peuvent pas l'être donc je ne vois pas l'intérêt de considérer un cas en plus..)
J'arrive avec des exemples simples (par exemple si leur PGCD est égal à 2, 3 ou 4, mais je n'arrive pas avec un diviseur d quelconque ), mais je ne vois pas de façon de procéder.. Du coup je vais continuer..!

[paquito]

Home, Sweet Home !
Je suis rentré il y un jour donc j'ai pu revoir un peu mes calculs en les posant !
Merci pour ces conseils, ils l'ont bien aidé
Donc j'ai bien réussi pour les cas où b divisent a et j'ai aussi montré que a et b ne sont pas premiers (donc que a n'est pas premier).

Considérons les cas où b divise a. Il existe donc un entier naturel non nul q tel que a=bq

On a alors:


Puisque c est un entier, q+1 divise bq.
Puisque q+1 divise bq, tous les facteurs premiers de q+1 apparaissent dans bq. Or PGCD(q+1; q)=1 (propriété de deux nombres consécutifs), donc aucun facteur premier de q+1 apparaît dans q, donc tous les facteurs premiers de q+1 apparaissent dans b, donc q+1 divise b.
Il existe donc un entier p tel que:
b=(q+1)p.
On en déduit que a=pq(q+1).

En remplaçant a et b par leur valeurs, on obtient c=pq. Puisque c est un entier naturel non nul pour tout p et q, on en déduit qu'il existe des solutions pour toutes les valeurs de p et de q.

Donc, pour tout entiers non nuls p et q, le tripler (pq(q+1); p(q+1); pq) est solution de (E).

On remarque aussi que:
donc il existe un d tel que et

J'ai aussi remarqué qu'il y avait des solutions où b ne divisait pas a, donc j'essaie de nouveau de généraliser mon résultat pour tout a et b non premiers entre eux (puisqu'ils ne peuvent pas l'être donc je ne vois pas l'intérêt de considérer un cas en plus..)
J'arrive avec des exemples simples (par exemple si leur PGCD est égal à 2, 3 ou 4, mais je n'arrive pas avec un diviseur d quelconque ), mais je ne vois pas de façon de procéder.. Du coup je vais continuer..!

Je vais te donner un petit coup de pouce parce que la solution générale n'est pas évidente à trouver:

Soient a et b 2 entiers naturels non nuls; il exite x et y tels que x^y=1 et b/a=y/x soit b=ax/y.....

[Waax22951]

Je vais te donner un petit coup de pouce parce que la solution générale n'est pas évidente à trouver:

Soient a et b 2 entiers naturels non nuls; il exite x et y tels que x^y=1 et b/a=y/x soit b=ax/y.....

N'est pas plutôt x^y=1 et a/b=x/y, soit a=bx/y ? (C'est juste pour être sûr qu'on parle de la même chose, pour éviter de partir en fausse piste, mais sinon je comprends..!)
Par contre je ne vois pas vraiment où tu veux en venir.. Puisque normalement, x doit être égal à 1..
Ou alors je ne parle pas du tout de la même fraction !
Nous parlons bien de ? (ou )

Merci tout de même ! :lol3:

[paquito]

Ca veut dire tout simplement que quels que soient les entier a et b il existe une fraction irréductible y/x telle que b/a=y/x. Tu peux bien sûr prendre a/b =x/y puisque a et b jouent des rôles symétriques. Mais cela permet d'affirmer que b=(y/x)a avec x^y=1 et cette relation est toujours vérifiée, donc on fait une étude générale. On parle de la fraction b/a; à toi de voir où cela conduit...

[Waax22951]

Ca veut dire tout simplement que quels que soient les entier a et b il existe une fraction irréductible y/x telle que b/a=y/x. Tu peux bien sûr prendre a/b =x/y puisque a et b jouent des rôles symétriques. Mais cela permet d'affirmer que b=(y/x)a avec x^y=1 et cette relation est toujours vérifiée, donc on fait une étude générale. On parle de la fraction b/a; à toi de voir où cela conduit...

Aaaah d'accord je n'avais pas du tout compris ça comme ça ! Merci beaucoup ! :lol3:
Du coup je vais voir ce que ça donne et je donnerai ma réponse le plus tôt possible ! :lol3:
Bonne soirée :we:

[Waax22951]

Alors j'ai réussi à obtenir un résultat qui semble fonctionner mais je me pose tout de même une question.. Je suis parti du fait que x et y soient premiers entre eux, et pourtant, au final, le résultat fonctionne pour tout x et pour tout y..!
Du coup je met ma réponse, si on pouvait m'éclairer, ce serait génial !


Remarque préliminaire: si , alors . Cette propriété découle de l'algorithme d'Euclide.
En effet, on a a-r=bq (avec ), donc a=bq+r. L'algorithme d'Euclide permet de conclure que .

On rappelle que pour tout entiers strictement positifs a et b, il existe deux entiers premiers entre eux x et y tels que .
On en déduit que: .
Or, on a aussi , donc . Donc .
Puisque c est un entier naturel, on en déduit que x+y divise xb. Or x+y et x sont premiers entre eux, donc le lemme de Gauss permet d'affirmer que x+y divise b. Il existe donc un entier p tel que b=p(x+y).
On a donc c=px.
On a aussi .
Donc , or a-px est un entier, donc y divise px². Or x et y sont premiers entre eux, donc x² et y le sont aussi. (En effet, si un nombre premier divise y mais ne divise pas x, il ne divise pas non plus x²). Le lemme de Gauss permet donc encore d'affirmer que y divise p. Il existe donc un entier z tel que p=yz.
On a finalement et .
On vérifie bien que:
. On a donc bien avec, pour tout entier x y et z non nuls, .

PS: Pour démontrer que [xz(x+y)]^2 + [yz(x+y)]^2 + [xyz]^2 est un carré parfait, je m'en occuperai après, je n'ai pas trop le temps en ce moment :/
Je préfère qu'on vérifie mes résultats et surtout qu'on m'explique pourquoi ça marche pour tout x y et z..!
(Je dirais qu'on peut affirmer que ça fonctionne pour tout x et y puisqu'on fait une vérification après, mais je ne suis vraiment pas sûr..)

Bonne journée ! :lol3:

[paquito]

Tu ne prends pas le chemin le plus court, mais tu as trouvé toutes les solutions. Bravo!

[Waax22951]

Tu ne prends pas le chemin le plus court, mais tu as trouvé toutes les solutions. Bravo!

Merci beaucoup pour cet exercice ! :lol3:

Bonne continuation !