Sylviel a écrit:Et qu'en est-il des polynomes périodiques ?
Un polynôme est selon moi dit périodique de période T si et seulement si, il existe un réel T tel que pour tout x :
=P(x))
Ca me fait d'ailleurs penser, avec les polynomes constant, on a bien pour tout x et pour tout réel
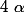
:
=P(x))
, donc les polynômes constant doivent-être périodiques.
Je parie que tu veux un exemple :
Si
=8)
alors
=8)
donc P est périodique de période 4, mais si
= 4)
alors
=4)
donc P est aussi périodique de période 7, donc je rajouterai qu'un polynôme P est périodique pour tout les réels.
Après je pense que les autres Polynome de degré supérieur à 1 ne sont pas périodiques.