Rappel cours Exponentielle [TS]

[LeFish]

Bonsoir a tous , j'avais une petite question , c'est comment dériver .

je sais que

Donc en dérivant ca donnerait
mais je suis pas sur ...

C'est pas dans le cours donc je sais pas ce que ca fait comme dérivée ^^.

Merci d'avance !

[Luc]

Salut,

Bonsoir a tous , j'avais une petite question , c'est comment dériver .

je sais que

Donc en dérivant ca donnerait
mais je suis pas sur ...

C'est pas dans le cours donc je sais pas ce que ca fait comme dérivée ^^.

Merci d'avance !

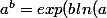Effectivement c'est ça à condition de bien placer les parenthèses. Mais il est complètement inutile de retenir ce genre de formules. Tout ce qu'il faut savoir c'est que par définition, . Tu connais ensuite la dérivée de

Il est inutile de connaître par cœur ce genre de formules, par contre il est indispensable de connaître, de comprendre et de savoir utiliser les formules de dérivation élémentaires pour pouvoir calculer la dérivée de n'importe quelle fonction construite à partir des fonctions usuelles.

Cordialement,

Luc

[MAC52]

Et puis surtout comme ça n'est pas du cours, on n'a même pas le droit de le citer, donc en soi ça ne sert à rien de l'apprendre.
De plus avec ton astuce d'écriture de u^v tu peux dériver que là où u est strictement positive...

MAC