Rapide question sur une somme de coeff. binomiaux
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Skrilax
- Membre Relatif
- Messages: 426
- Enregistré le: 14 Juin 2008, 13:49
-
 par Skrilax » 08 Mar 2009, 12:52
par Skrilax » 08 Mar 2009, 12:52
Bonsoir,
Je viens de rencontrer quelque chose qui m'empêche de continuer dans un exercice.
Quelqu'un saurait m'indiquer comment je calcule

?
Merci
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 08 Mar 2009, 13:39
par Timothé Lefebvre » 08 Mar 2009, 13:39
Salut, tiens ça me dit quelque chose ça.
L'énoncé ne serait-il pas :
Soit

Montre rque pour tout x différent de 1
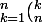P_k(x) = 2^{n-1}P_n(\frac{1+x}{2}))
?
Au passage, la notation

n'est plus à l'ordre du jour parait-il

-
Skrilax
- Membre Relatif
- Messages: 426
- Enregistré le: 14 Juin 2008, 13:49
-
 par Skrilax » 08 Mar 2009, 13:43
par Skrilax » 08 Mar 2009, 13:43
Non ce n'est pas cet énoncé :)
Et pour la notation, ben il faut croire que si ^^
Et puis de toute façon je ne sais pas écrire les ( ) en latex :)
PS = (pour la notation ( ), c'est le n qui est au dessus du k )
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 08 Mar 2009, 13:48
par Timothé Lefebvre » 08 Mar 2009, 13:48
J'ai modifié ouais, pour la notation on m'a déjà fait la remarque !
Dommage il est marrant ce problème !
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Mar 2009, 16:01
par Zweig » 08 Mar 2009, 16:01
Salut,
Ton expression vaut

.
Pour cela, utilise le fait que pour tout
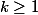
:
[CENTER]
 = n \left(\begin{array}{c}<br />n-1\\<br />k-1\end{array}\right))
[/CENTER]
-
Skrilax
- Membre Relatif
- Messages: 426
- Enregistré le: 14 Juin 2008, 13:49
-
 par Skrilax » 08 Mar 2009, 17:18
par Skrilax » 08 Mar 2009, 17:18
Ah super merci pour la relation :++:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Mar 2009, 17:28
par Zweig » 08 Mar 2009, 17:28
Au plaisir :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités