Bonjour,
alors voilà nous sommes actuellement dans le chapitre des suites et comme vous pouvez le voir dans le titre c'est le raisonnement par récurrence qui me pose problème surtout dans l'exercice suivant:
Exercice:
1) Déterminer à partir de quel rang la propriété Pn: 2^n>= (n+2)^2 semble vraie.
2) Démontrer alors par récurrence que la propriété est vraie à partir du rang trouvé.
Alors, pour la première question j'ai entré les suites dans ma calculatrice, puis cherché le rang à partir duquel la propriété Pn semble vraie, il s'agit du rang n=6.
Pour la seconde question j'ai mis dans l'initialisation que la propriété était vraie pour tout n>= 6
(c'est à dire d'une part 2^6=64 , et d'autre part (6+2)^2=64.
Donc la propriété Pn est vraie au rang n=6)
Mais c'est au niveau de l'hérédité que je bloque à cause de l'inégalité et qu'il faut prouver que c'est à partir d'un rang que Pn+1 est vraie.
Ce que j'ai déjà écrit:
Hérédité:
On suppose que Pn est vraie au rang n=6 donc on souhaite démontrer que Pn+1 est vraie,
i.e. : 2^(n+1) >= (n+1+2)^2
<=>2^(n+2) >= (n+3)^2
<=>2^n + 2 >= n^2+6n+9
<=>2^n >= n^2+6n+9-2
<=>2^n >= n^2+6n+7
Et là je bloque je me dis que peut être ce n'est pas pour rien qu'il y a un 6 qui apparaît vu qu'il faut prouver que la propriété lors de la récurrence est vraie à partir du rang n= 6.
Donc si il y aurait quelqu'un pour m'aider, je serai toute ouïe.
Merci d'avance!
Raisonnement par récurrence (suite)
4 messages
- Page 1 sur 1
Re: Raisonnement par récurrence (suite)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Raisonnement par récurrence (suite)
salut
tu supposes^2)
tu dois démontrer:
^2)
or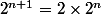
^2) d'après l'hypothèse de récurrence
d'après l'hypothèse de récurrence
tu as donc à prouver que
^2\geq (n+3)^2)
ce qui est facile
tu supposes
tu dois démontrer:
or
tu as donc à prouver que
ce qui est facile
Re: Raisonnement par récurrence (suite)
Bonjour à vous,
merci pour l'aide apportée, j'y vois plus clair maintenant!!
merci pour l'aide apportée, j'y vois plus clair maintenant!!
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 115 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
