Raisonnement par récurence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 15 Nov 2006, 17:12
par Zebulon » 15 Nov 2006, 17:12
Bonjour,
c'est
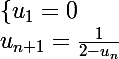
?
Alors
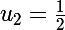
mais
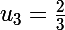
et heureusement que

car sinon, comment serait défini
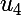
?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 15 Nov 2006, 17:26
par Zebulon » 15 Nov 2006, 17:26
Ca permet de conjecturer une expression de

en fonction de n.
Je les écris à la suite :
;

;

;

;

;

; ... ?
Vous ne remarquez rien ? Qu'est-ce qu'on aimerait que ce soit après ?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 15 Nov 2006, 17:27
par Zebulon » 15 Nov 2006, 17:27
Célia-1ereES a écrit:En fait j'ai trouvé! Un = n-1/n ! Enfin je crois..
C'est ça. Maintenant, prouvez-le !
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 15 Nov 2006, 17:42
par Zebulon » 15 Nov 2006, 17:42
De rien. Comment faîtes-vous ?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 15 Nov 2006, 17:50
par Zebulon » 15 Nov 2006, 17:50
C'est la méthode. Si vous voulez, montrez-moi comment comment vous faîtes, je vous corrigerai.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 15 Nov 2006, 18:01
par Zebulon » 15 Nov 2006, 18:01
Célia-1ereES a écrit:J'ai vérifié et en fait ça marche pas. Comment retrouver Un+1 = n-1/n en partant de Un+1 = 1 / 2-Un ?
Ca ne marche pas parce que ce n'est pas
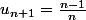
, mais c'est
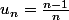
.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 15 Nov 2006, 18:15
par Zebulon » 15 Nov 2006, 18:15
Ce n'est comme ça qu'il faut s'y prendre.
On veut montrer que si
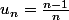
(c'est l'
hypothèse de récurrence), alors
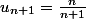
, en utilisant le "lien" entre

et

, à savoir
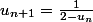
. Jusque-là, ça va ?
Pour le montrer, on part de
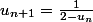
. Comme on suppose que
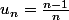
, on peut remplacer

par

dans
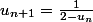
. Il faut qu'on arrive à
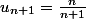
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités