Raisonnement par absurde.

[Okamyne]

Bonjour, j'aimerai bien un peu d'aide pour ce problème que je n'arrive pas a assimiler,
On se donne n+1 rêel x0 ,x1 ,x2 , . . . ., xn de [0,1] n≥1
vérifiant 0≤ x1≤ x2≤ .....≤ xn≤ 1
Montrez qu'il y'a deux de ces réels qui sont distants de moins de 1/n.
Il faudrait utiliser le raisonnement par absurde.
Voilà j'espère recevoir de l'aide de votre part.

[titine]

Bonjour, j'aimerai bien un peu d'aide pour ce problème que je n'arrive pas a assimiler,
On se donne n+1 rêel x0 ,x1 ,x2 , . . . ., xn de [0,1] n≥1
vérifiant 0≤ x1≤ x2≤ .....≤ xn≤ 1
Montrez qu'il y'a deux de ces réels qui sont distants de moins de 1/n.
Il faudrait utiliser le raisonnement par absurde.
Voilà j'espère recevoir de l'aide de votre part.

Ne serait ce pas plutôt des inégalités strictes :
0<x1<x2<....<xn<1
Car sinon on peut avoir par exemple x1=x2=x3=...=xn=0 et alors la distance entre 2 de ces réels est 0

Si on a 0<x1<x2<....<xn<1
Si on suppose que la distance entre x1 et x2 > 1/n
Ainsi que celle entre x2 et x3
Ainsi que celle entre x3 et x4
....
Ainsi que celle entre x(n-1) et xn
Alors la distance entre x1 et xn sera supérieure à n*1/n = 1
Ce qui est impossible puisque tous ces nombres sont entre 0 et 1
Donc il y a au moins une de ces distances qui est inférieure à 1/n.

[Okamyne]

Bonsoir titine, non l'exercice est bien tel quel, il faudrait aussi le résoudre à l'aide du raisonnement par absurde.
Merci pour ta réponse.

[zygomatique]

salut

non c'est bien des inégalités larges ...

soit n + 1 réels tels que


raisonnement par l'absurde : supposons que pour tout n = 0, 1, 2, ..., n-1 :



...

[beagle]

inégalités larges dans 0,1 ouvert pas fermé alors, non?

n=2, donc 3 réels, si c'est 0 et 1 compris , je me sers: 0 , 1/2, 1
lesquels distants de moins de 1/2?

[zygomatique]

1/2 est moins de 1/2 ...mais pas strictement moins de 1/2 ...

[beagle]

1/2 est moins de 1/2 ...mais pas strictement moins de 1/2 ...

ah OK, ben c'est délicat d'utiliser le français alors, mieux vaut mettre des symboles mathématiques.

Je vais essayer chez ma boulangère de lui acheter moins d'une baguette, oui, oui, celle là en entier c'est ce que je vous ai demandé!
Tu partages 9 bonbons pour trois enfants, 3 bonbon chacun, et l'enfant le plus mathématicien te répond: pourquoi j'en ai moins que les autres.Hé man, t'en as pas strictement moins; t'en as juste moins comme les autres.Vous en avez tous moins faites pas ch..r.

[zygomatique]

et oui mais c'est cela qui fait la distinction entre < et =< et leur définition propre qui en français "maladroit" conduit à ces ambiguités

j'ai appris tout petit :

un nombre a est plus petit qu'un nombre b et on écrit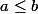 s'il existe un nombre positif k tel que a + k = b

et k = 0 est positif ...

dans ton exemple on peut donc aussi conclure qu'il en plus que les autres (puisque 0 est négatif) ... alors faites pas c... les mômes ...

[beagle]

et oui mais c'est cela qui fait la distinction entre < et =< et leur définition propre qui en français "maladroit" conduit à ces ambiguités

j'ai appris tout petit :

un nombre a est plus petit qu'un nombre b et on écrit s'il existe un nombre positif k tel que a + k = b

et k = 0 est positif ...

dans ton exemple on peut donc aussi conclure qu'il en plus que les autres (puisque 0 est négatif) ... alors faites pas c... les mômes ...

je m'incline au niveau de la définition mathématique, pour autant je ne trouve pas le français maladroit lorsqu'il dit plus moins et égal.C'est le français qui est le plus clair car pas d'intersection de situation.
La définition mathématique pouvait s'écrire il existe un k positif non nul, elle est avec k positif et zéro est positif ...

[beagle]

surtout que zéro positif, est-il moins négatif?
c'est peut-être pratique pour racine carré de zéro,mais sinon sur le web on trouve ceci à zéro positif ou négatif:
Les nombres positifs sont les réels x tels que x>=0
Les nombres négatifs sont les réels x tels que x<=0

Mais il n'est ni STRICTEMENT positif , ni STRICTEMENT négatif.

donc c'est pénible d'avoir la definition du inf qui dépend de k qui dépend de inf
bon alors faut reprendre toutes les défintions construites une par une et je m'en tape de cette problématique,
Voili Voilo ....

[zygomatique]

en fait on subit l'influence des (de cette saleté d'anglo-saxons (je plaisante)) pour qui inférieur se traduit par < et =< par inférieur ou égal

alors qu'en France on dit (on disait) inférieur pour =< et inférieur strictement pour < ... (c'est du moins ce que j'ai appris et je trouve cela cohérent dans tous les cas que j'ai rencontrés et il y en a)

[Dasson2]

Je crois que ces difficultés de vocabulaire viennent des "maths modernes" ou le mot "inférieur", par exemple, était à prendre au sens large pour que la relation soit réflexive.
Pendant des années, le mot a été pris au sens large par certains, au sens strict par d'autres...
Je cois qu'il vaut mieux utiliser "inférieur ou égal à" ou bien "inférieur strictement à".

[zygomatique]

oui voila un exemple très parlant : la réflexivité ...

et encore oui malheureusement ... vu la médiocrité du français chez beaucoup de jeunes (elle-même due à la médiocrité du système éducatif actuel)