Raisonne ment par recurence

[muanamayele98]

Bonsoir, je suis bloqué a un exercices :mur: dont voici l'énoncé
1- Démontrer par récurrence que pou tout n appartenant a N*:
1^3+2^3+3^3+....+n^3= (n^2(n+1)^2)/4

Si quelqu'un puvais m'expliquer ca serait gentil :++: :lol3:

[capitaine nuggets]

Salut !

As-tu déjà fait l'initialisation ?
Où bloques-tu ?

[muanamayele98]

Salut !

As-tu déjà fait l'initialisation ?
Où bloques-tu ?

Ouiv mais je suis pas sure j'ai calculer pour n=0

avec la formule ca me donne ( 0^3 ( 0+1)^2)/4 =0

et on sait que 0^3= O
donc la proprietée est vrai pour n=0

Je voulais faire pour n=1 ce n'est pas mieux ?
J'a chercher l'herédité apres:

Sk= (k2(K+1)2)/4
et Donc on a Sk+1=13+23+33+.........+k3
Sk +n3

[capitaine nuggets]

Déjà, appartient à 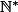donc l'initialisation se fait au rang :++: .
Ensuite, j'ai un peu de mal à te lire pour l'hérédité.
En bref, suppose l'égalité que tu veux montrer vraie pour un certain rang ; montre qu'alors cette même égalité est vraie au rang k+1 et ceci en utilisant l'égalité au rang k supposée vraie au préalable.

:+++:

[muanamayele98]

Pour l'hérédité j'ai mis ceci
Sk= (k^2(K+1)^2)/4
et que au rang k+1 on a :=1^+2^3+3^3+.........+(k+1)^3
Sk +n^3
[ (k^2(K+1)^2)/4 ] +n^3

[muanamayele98]

Déjà, appartient à donc l'initialisation se fait au rang :++: .
Ensuite, j'ai un peu de mal à te lire pour l'hérédité.
En bref, suppose l'égalité que tu veux montrer vraie pour un certain rang ; montre qu'alors cette même égalité est vraie au rang k+1 et ceci en utilisant l'égalité au rang k supposée vraie au préalable.

:+++:

Mais apres je sais pas quoi faire :/

[titine]

On suppose que : 1^3 + 2^3 + 3^3 +.... + k^3= (k² (k+1)²)/4
Et on doit démontrer qu'alors : 1^3 + 2^3 + 3^3 +....+ (k+1)^3= ((k+1)² (k+1+1)²)/4

1^3 + 2^3 + 3^3 +....+ (k+1)^3 =1^3 + 2^3 + 3^3 +....+ k^3 + (k+1)^3
Et ceci est égal, d'après notre supposition, à :
= (k² (k+1)²)/4 + (k+1)^3
Tu suis ?
Il faut maintenant que tu vérifies que ceci est égal à ((k+1)² (k+1+1)²)/4
En mettant (k+1)² en facteur tu dois t'en sortir

[muanamayele98]

j'ai developpeé l'expression pour le rang k+1 et ca me donne:
(k^4+6k^3 +13k² +12k+4)/ 4
et j'ai mis (k+1)² en facteur et ca me donne (k+1)²(k+2)² /4l ce

donc cela reviens a notre
egalité que l'on devait trouvé au rang k+1 soit :
que ceci est égal à ((k+1)² (k+1+1)²)/4

est ce bon ou?

[SimonY]

Tu prends la somme avec les cubes, tu lui rajoutes (k+1)^3 et tu rajoutes ça au second membre de l'équation : au truc que tu supposes vrais.
Tu mets ça au même dénominateur, tu ajoutes tous les termes.

D'un aure côté, tu développes ce que tu dois démontrer pour arriver à des sommes de degré, et tu a normalement la même chose que le truc du haut

[muanamayele98]

Euh j'ai pas compris ...

[titine]

j'ai developpeé l'expression pour le rang k+1 et ca me donne:
(k^4+6k^3 +13k² +12k+4)/ 4
et j'ai mis (k+1)² en facteur et ca me donne (k+1)²(k+2)² /4l ce

donc cela reviens a notre
egalité que l'on devait trouvé au rang k+1 soit :
que ceci est égal à ((k+1)² (k+1+1)²)/4

est ce bon ou?

Tout à fait.
Tu as montré que
si 1^3 + 2^3 + 3^3 +....+ k^3 = (k² (k+1)²)/4 est vraie
alors 1^3 + 2^3 + 3^3 +....+ (k+1)^3 = ((k+1)² ((k+1)+1)²)/4 est vraie
Tu as bien prouvé que si tu supposes ta propriété vraie au rang k alors elle est aussi vraie au rang k+1.
Donc ta propriété est bien héréditaire.

[muanamayele98]

D'accord Merciiii de votre aide )