Radical et Expression Conjugée !

par **azerty67sang** » 13 Déc 2006, 19:11

Bonsoir , j'ai besoin d'aide ( c'est pour demain )
le voici :

dans le 3) , j'ai deja fait : racine3 - racine5
racine5 +3
2 - racine3
mais le reste j'arrive pas , surtout le 4)

Merci de m'aidé
A bientot !

par **fonfon** » 13 Déc 2006, 19:35

salut,

ecris que 1+2V3=(1)+(2V3) tu devrais trouver l'expresssion conjuguée,de même pour les autres mais des parenthéses si tu ne vois pas directement

par **azerty67sang** » 13 Déc 2006, 19:45

1+2V3= 1-2V3 ??
2V5+V2 = 2V5-V2 ???
a-bVc = a+bVc ???

ps : et pour le 4)

par **fonfon** » 13 Déc 2006, 19:58

1+2V3= 1-2V3 ??
2V5+V2 = 2V5-V2 ???
a-bVc = a+bVc ???

voilà,c'est çà n'oublie pas il t'en reste encore une

je te montre le J)

par **azerty67sang** » 13 Déc 2006, 20:02

fonfon a écrit:voilà,c'est çà n'oublie pas il t'en reste encore une

je te montre le J)

Mais comment avez-vous fait? pour passé de 2-V3 à (2-V3)(2+V3) comment avez-vous faire ? ^^

par **fonfon** » 13 Déc 2006, 20:07

on te demande d'ecrire les nombres sans radical au denominateur donc il faut utiliser l'expression conjuguée pour faire disparaitre le(s) radical(ux)

par **azerty67sang** » 13 Déc 2006, 20:12

Alors pour le K , la reponse est :

V2 ......................... V2
------------- = -----------
(V2)² + (V7)²............9

Dites moi si j'ai juste !
ps : comment faire les racines carrés sur l'ordinateur ?

par **fonfon** » 13 Déc 2006, 20:18

Alors pour le K , la reponse est :

V2 ......................... V2
------------- = -----------
(V2)² + (V7)²............9

Dites moi si j'ai juste !

non,c'est pas bon il faut multiplier le denominateur et le numerateur par l'expression conjuguée pour ne pas changer le sens de l'expression donc

c'est

au numerateur

ps : comment faire les racines carrés sur l'ordinateur ?

http://www.ilemaths.net/guide-latex.php

par **azerty67sang** » 13 Déc 2006, 20:24

Donc cela fait :

2-2

--------------------------
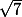
5

C'est sa ?

par **fonfon** » 13 Déc 2006, 20:34

non,c'est pas ça

tu peux developper le numerateur si ça te chante mais là tu remarques que lon a plus de radical au denominateur

par **fonfon** » 13 Déc 2006, 20:37

bon moi, je vais manger je reviendrais sûrement après sinon quelqu'un peut prendre la suite

par **azerty67sang** » 13 Déc 2006, 20:41

Ah oui le moins devant le 5 je l'ai oublié ^^

Pour le L : reponse :

3(2V5+4)
=-------------------
(2V5 + 4) ( 2V5-4)

.......3(2V5+4)
= --------------
....(2V5)² - (4)²

.....3(2V5+4)
=-------------
.......-6

C'est juste ?

par **fonfon** » 13 Déc 2006, 20:56

presque
c'est:

3(2V5-4)
=-------------------
(2V5 + 4) ( 2V5-4)

par **fonfon** » 13 Déc 2006, 21:00

c'est juste jusqu'ici

Pour le L : reponse :

3(2V5+4)
=-------------------
(2V5 + 4) ( 2V5-4)

.......3(2V5+4)
= --------------
....(2V5)² - (4)²

apres ça donne

par **azerty67sang** » 13 Déc 2006, 21:08

Pour le M j'en est aucune aidée :hein3:
Il faut faire la meme chose ?

Ps: Merci Fonfon pour ton aide !

par **fonfon** » 13 Déc 2006, 21:15

oui,il faut faire la même chose

=

=...

par **azerty67sang** » 13 Déc 2006, 21:20

Donc si je ne trompe pas , cela fait :

18
----
18

= 1 :hum:

par **fonfon** » 13 Déc 2006, 21:27

non,c'est pas bon

...=

=

voilàje te conseille de revoir tout ça à tête reposée

A+

par **azerty67sang** » 13 Déc 2006, 21:31

Ah oui faut utilisé l'identité remarquable : (a-b)² = a² - 2ab + b²
Merci pour ton aide Fonfon , un grand merci a toi ! :id:

Radical et Expression Conjugée !

Radical et Expression Conjugée !

Qui est en ligne