Racines d'un polynôme

[julie1234]

Bonjour,

Comment trouver les racines de ce polynôme : 4x^3 + 24x^2 + 41x + 21 ? Je sais que ce polynôme a pour racine -1 mais comment le trouver ? Par la méthode de la racine évidente ?

[Miloud]

bonsoir , oui tu peux faire ça la methode du racine évidente , ou bien tu décompose ce plynome en deux facteur , un son degré égale 1 ,et l'autre son degré égale a 2 c-a- d
4x^3 + 24x^2 + 41x + 21 = ( 4x+a)( x^2+bx+c) tu developpe , puis tu compare les constants de chaque degré avec les constants que tu a dans le plynome , ce qui te donne a, b et c , le reste est facile je pense julie1234 .

[Dinozzo13]

Salut !
Le polynôme admet pour racine 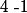donc par conséquent est factorisable par
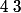Le polynôme étant de degré est factorisable par qui est du premier degré, on en déduit donc qu'il existe un trinôme tel que pour tout x réel :

avec
Cherchons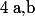 et 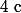en procédant par identification, pour tout réel x :
.
En développant le membre de droite tu regroupe tous les termes en "" de chaque degré ainsi que des termes constant :

Or deux polynômes sont égaux si et seulement si ils ont le même degré et leurs coefficients sont égaux. Il vient donc :

Tu connais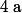 et 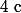, tu détermines donc facilement .
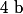Par conséquent
Ainsi tu résous .
Tu en déduis une factorisations de et donc du polynôme .

[Le_chat]

Bonjour,

Comment trouver les racines de ce polynôme : 4x^3 + 24x^2 + 41x + 21 ? Je sais que ce polynôme a pour racine -1 mais comment le trouver ? Par la méthode de la racine évidente ?

Si tu as vu que -1 est racine évidente, tu le marques dans ta copie EN JUSTIFIANT et c'est bon. (du genre: -1 est racine evidente, en effet,
4(-1)^3+24(-1)^2+41(-1)+21=...=0)
Donc ton polynôme admet pour racine -1, il est factorisable par (x+1)... et tu regardes le message d'au dessus pour la suite.