Questions sur les complexes

[Dinozzo13]

Bonjour, en lisant un livre, je me suis demandé comment écrire plus simplement ou sous forme algébrique ?
Est-il réel ? ou imaginaire pur ?

[Anonyme]

Réel non ?

[Dinozzo13]

Ah, je crois avoir trouvé :
On sait que donc .
Cela paraît-il exact ?

[Dinozzo13]

Si c'est bon, une autre question m'est venue : comment écrire plus simplement ou alors sous forme algébrique ?

[Dinozzo13]

Et puis, comment est-il possible de calculer des puissances complexes du genre : ?

[Skullkid]

C'est quoi ta définition d'un complexe élevé à une puissance complexe ? C'est quoi ? Es-tu sûr que ?

[Dinozzo13]

Ben, c'est ce que j'ai pensé, mais j'ai jamais dit en être sûr.
Ce que je vois comme un complexe élevé à une puissance complexe, est une expression de la forme où et appartiennent à
Comme ça par exemple :

[ned aero]

salut,

pour i, c'est peut être mieux de passer par l'exponentielle je pense

[Dinozzo13]

Salut ! C'est-à-dire ?

[Skullkid]

Ce que je vois comme un complexe élevé à une puissance complexe, est une expression de la forme où et appartiennent à

Oui d'accord, mais là tu ne définis rien. Tu dis juste "je vais élever le complexe a à la puissance b, et je vais noter le résultat ". Mais on n'a aucune idée de ce que peut bien valoir . Avant de vouloir faire des calculs sur des objets, il faut définir les objets en question, et les règles qui s'y appliquent. As-tu une définition à proposer pour ?

[Ben314]

En fait, on peut définir de façon assez "sereine" 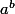lorsque :
1) a est en complexe quelconque et b un entier naturel non nul.
2) a un complexe non nul et b un entier relatif quelconque.
3) a est un réel strictement positif et b un complexe quelconque.

Dans tout les autres cas, les tentatives de définition ne sont que trés peu satisfaisantes (on n'a pas les propriétés que l'on aimerais avoir, c'est à dire et ).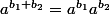
Pour donner un exemple,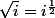 n'est pas clairement défini car il existe deux complexes distincts vérifiant 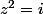et il n'y a aucune raison particulière de privilégier l'un des deux comme étant LA racine carré de i (par contre, on peut dire que ces deux complexes sont LES racines carrées de i)