Question sur le cours des fonctions dérivées

[Clemzd]

Bonjour à tous !

Il y a une question que je me pose sur les nombres dérivées : on dit que le nombre dérivée c'est le coefficient directeur de la tangente à f, lorsque il existe une limite finie pour ce nombre lorsque h tend vers 0 (a+h étant l'intervalle choisi sur la fonction).

La dérivée c'est donc le coefficient directeur de l'approximation affine (la tangente) donc ce que je ne comprend pas c'est comment on peut se retrouver avec des dérivées donnant des fonctions qui ne sont pas des "droites", car une tangente est toujours comme une droite...

Merci d'éclairer ma lanterne les amis :)

[Luc]

Bonjour,

en chaque point a, il y a une tangente à f en a qui est une droite, mais toutes ces droites n'ont pas forcément le même coefficient directeur.

C'est le nombre dérivé qui est le coefficient de la tangente.
La fonction dérivée, c'est la fonction qui à un point associe le nombre dérivé de la fonction en ce point.

[Clemzd]

D'accord donc la fonction dérivée permet de retrouver le coefficient directeur à la tangente en un point et un seul ?

[Luc]

D'accord donc la fonction dérivée permet de retrouver le coefficient directeur à la tangente en un point et un seul ?

La connaissance de la fonction dérivée f' sur un ensemble permet de retrouver le coefficient directeur de la tangente à Cf en tous les points de cet ensemble.

[Anonyme]

@Clemzd
Ce qu'il faut comprendre :
la notion de nombre dérivé de f en est lié à
l'existence d'une limite finie du taux de variation de la fonction sur les 2 segments [a , a+h] et [a-h , a] avec h >0
On dit alors que la fonction f est dérivable en

Ce nombre qu'on note est bien le coefficient directeur de la tangente à la courbe représentative de f dans un repère donné

Puis ensuite on peut créer la notion de fonction dérivée en créant une nouvelle fonction qui à
--> cette limite finie quand appartient à un segment [A,B] donné ( il faut que f soit dérivable )
et on note cette nouvelle fonction

Attention
Il existe des fonctions comme f(x)= | x | (valeur absolue de x ou ABS(x))
qui ne sont pas dérivable en un point (dans cet exemple la fonction f n'est pas dérivable en 0)

MAIS cette fonction est dérivable à droite et est dérivable à gauche en 0
c'est à dire en et en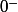
et sa courbe admet 2 tangentes...

Cela vient du fait que
1) la limite du taux de variation en de la fonction f est finie (limite qui vaut +1)
2) la limite du taux de variation en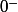 de la fonction f est finie (limite qui vaut -1)
3) que ces 2 limites ne sont pas égales

A méditer...