Question de raisonnement
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 10 Oct 2006, 21:00
par sue » 10 Oct 2006, 21:00
salut,
j'ai un petit probleme avec cette limite :
(x-b)}{x^2+x})
je dois déterminer la limite selon les valeurs des paramètres a et b , mais je sais pas quel cas dois-je étudier ? ..je pense qu'il faut commencer par :
-si
 ou
ou 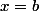
puis la négation : -si
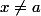 et
et 
.
une piste ?
MERCI.
 par Dominique Lefebvre » 10 Oct 2006, 21:14
par Dominique Lefebvre » 10 Oct 2006, 21:14
sue a écrit:salut,
j'ai un petit probleme avec cette limite :
(x-b)}{x^2+x})
je dois déterminer la limite selon les valeurs des paramètres a et b , mais je sais pas quel cas dois-je étudier ? ..je pense qu'il faut commencer par :
-si
 ou
ou 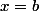
puis la négation : -si
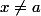 et
et 
.
une piste ?
MERCI.
Bonsoir,
Si tu choisis x = a ou x = b, le numérateur s'annule et l'étude n'a pas beaucoup d'intérêt (quelque soit x, la limite est nulle, puisque le numérateur est nul)
Tu dois étudier la limite de ta fonction quand x tend vers -1. Moi, je chercherais ce qui ce passe selon différentes valeurs de a et b dans le numérateur lorsque x tend vers -1...
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 10 Oct 2006, 21:15
par Flodelarab » 10 Oct 2006, 21:15
la seule question est si a=-1 ou b=-1
sinon la limite est toujours 0
ok?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 10 Oct 2006, 21:20
par sue » 10 Oct 2006, 21:20
Si tu choisis x = a ou x = b, le numérateur s'annule et l'étude n'a pas beaucoup d'intérêt (quelque soit x, la limite est nulle, puisque le numérateur est nul)
mais si le numérateur s'annulle nous aurons une forme indétrminée ''
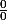
'', car le dénominateur s'annule tj qd

non?
 par Dominique Lefebvre » 10 Oct 2006, 21:23
par Dominique Lefebvre » 10 Oct 2006, 21:23
Tu peux aussi essayer de développer le numérateur et regarder ce qui se passe... Il y a un phénomène intéressant pour les couples (-1,0) et (0,-1)..
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 10 Oct 2006, 21:24
par sue » 10 Oct 2006, 21:24
Flodelarab a écrit:la seule question est si a=-1 ou b=-1
sinon la limite est toujours 0
ok?
c vrai ?! et si a=0 ou b=0 ?
 par Dominique Lefebvre » 10 Oct 2006, 21:26
par Dominique Lefebvre » 10 Oct 2006, 21:26
sue a écrit:mais si le numérateur s'annulle nous aurons une forme indétrminée ''
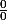
'', car le dénominateur s'annule tj qd

non?
très juste! Et alors, tu t'en sors comment de cette indétermination?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 10 Oct 2006, 21:36
par sue » 10 Oct 2006, 21:36
Dominique a écrit:très juste! Et alors, tu t'en sors comment de cette indétermination?
je pense s'il ya une F.I le dénominateur doit etre divisible soit par x ou (x+1) i.e soit (a=0 ou b=0 ) soit (a=-1 ou b=-1)
c'est ça ?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 10 Oct 2006, 21:37
par Flodelarab » 10 Oct 2006, 21:37
sue a écrit:c vrai ?! et si a=0 ou b=0 ?
si a= 0 ou b= 0 alors x-a (respectivement x-b) est égal à -1 et il n'ya pas d'indétermination
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 10 Oct 2006, 21:40
par sue » 10 Oct 2006, 21:40
Flodelarab a écrit:si a= 0 ou b= 0 alors x-a (respectivement x-b) est égal à -1 et il n'ya pas d'indétermination
y a pas d'intermination ok ..mais ça sera pas 0 !
Flodelarab a écrit:la seule question est si a=-1 ou b=-1
sinon la limite est toujours 0
ok?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 10 Oct 2006, 21:43
par Flodelarab » 10 Oct 2006, 21:43
sue a écrit:y a pas d'intermination ok ..mais ça sera pas 0 !

si ya pas indétermination alors quel est la limite ?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 10 Oct 2006, 21:53
par Flodelarab » 10 Oct 2006, 21:53
ya 3 limites différentes:
a+1
b+1
et 0
a toi de les reclasser en fonction de a et b
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 10 Oct 2006, 21:55
par sue » 10 Oct 2006, 21:55
si ya pas indétermination alors quel est la limite ?
SI a=0 ou b=0 la limite à gauche de -1 vaut

selon le signe du dénominateur .
pareil pour la limite à droite .
non?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 10 Oct 2006, 22:04
par Flodelarab » 10 Oct 2006, 22:04
sue a écrit:SI a=0 ou b=0 la limite à gauche de -1 vaut

selon le signe du dénominateur .
pareil pour la limite à droite .
non?
Oops
faute.
Je voulais bien sur dire:
Les 4 limites possibles sont
a+1
b+1


merci de m'avoir corriger
ceci dit, cela tend vers l'infini (+ ou -) quelque soit a et b différents de -1
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 10 Oct 2006, 22:09
par sue » 10 Oct 2006, 22:09
merci beaucoup à toi également et à Dominique Lefebvre :we:
@+
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 10 Oct 2006, 22:13
par Flodelarab » 10 Oct 2006, 22:13
sue a écrit:merci beaucoup à toi également et à Dominique Lefebvre :we:
@+
Tu ne nous donne pas ta réponse finale ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 10 Oct 2006, 22:17
par sue » 10 Oct 2006, 22:17
Re,
si je vous dérange pas j'ai une autre limite qui me pose probleme :

je voudrais juste savoir si en posant
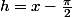
j'obtiendrais qq chose ...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 10 Oct 2006, 22:26
par sue » 10 Oct 2006, 22:26
Tu ne nous donne pas ta réponse finale ?
ça tend vers (+ ou - infinity ) si a=0 ou b=0 (il faut étudier la limite à gauche et à droite de -1)
si a=-1 cela tend vers 1+b et si b=-1 ça tend vers 1+a .
sinon cela tend aussi vers +ou - infini car le dénominateur ne s'annule pas . (ça revient au 1er cas)
c ça ?
merci
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 10 Oct 2006, 22:35
par Flodelarab » 10 Oct 2006, 22:35
sue a écrit:ça tend vers (+ ou - infinity ) si a=0 ou b=0 (il faut étudier la limite à gauche et à droite de -1)
si a=-1 cela tend vers 1+b et si b=-1 ça tend vers 1+a .
sinon cela tend aussi vers +ou - infini car le dénominateur ne s'annule pas . (ça revient au 1er cas)
c ça ?
oui et non.
c trop fouilli. pkoi a=0 et b=0 ... t'y tiens ... ces valeurs n'ont rien de spéciales.
quand est ce que c'est + infini et quand est ce que c'est -infini ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 10 Oct 2006, 22:49
par sue » 10 Oct 2006, 22:49
quand est ce que c'est + infini et quand est ce que c'est -infini ?
d'abord il faut étudier la limite à gauche et à droite de -1.
aprés il faut déterminer le signe de (a+1)(b+1) (positif si (a>-1 et b>-1)ou(a-1)ou(a>-1 et b<-1) respectivement (b<-1et..) .
c ça ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
ou
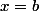
et
.