Question de raisonnement

[Flodelarab]

d'abord il faut étudier la limite à gauche et à droite de -1.
aprés il faut déterminer le signe de (a+1)(b+1) (positif si (a>-1 et b>-1)ou(a-1)ou(a>-1 et b<-1) respectivement (b<-1et..) .


c ça ?

Ya des idées.
Et le dénominateur ?

[sue]

Et le dénominateur ?

ben le dénominateur s'annulle tj qd ...reste à voir si c'es 0+ ou 0- (0- qd et 0+ qd )

donc qd
-si (a+1)(b+1)>0 --- ça tend vers -oo
_ sinon ça tend vers +oo

qd
-si (a+1)(b+1)>0 --- ça tend vers +oo
-sinon ça tend vers -oo

[Flodelarab]

Re,

si je vous dérange pas j'ai une autre limite qui me pose probleme :



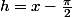
je voudrais juste savoir si en posant j'obtiendrais qq chose ...

Est ce que tu connais la limite en l'infini du quotient de 2 polynomes ?
tu ne gardes que les plus haut degré.

si tu connais, alors factorise par 1-sin(x) en haut et en bas.
Simplifie.
et pose X=cos(x)/(1-sin(x))
tu obtiens (1+X)/(1-X) qui a évidemment une limite de -1 quand X tend vers l'infini

ok?

[Flodelarab]

(0- qd et 0+ qd )

C le contraire

[sue]

Est ce que tu connais la limite en l'infini du quotient de 2 polynomes ?
tu ne gardes que les plus haut degré.

je sais ça mais je cherche pas la limite en l'infini mais qd ..sinon qq chose m'echape .

[Flodelarab]

je sais ça mais je cherche pas la limite en l'infini mais qd ..sinon qq chose m'echape .

oui ! Ce qui t'echappe c que ton X tend vers l'infini quand 1-sin(x) tend vers 0 quand x tend vers Pi/2

[sue]

oui j'ai remarqué ça mais X= cos(x)/1-sin(x) ...je vois une F.I moi qd :triste:

[sue]

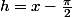
j'ai tenté en posant mais à la fin ça me donne un truc bizzare 1/h donc il faut avoir soit h tends vers 0+ ou 0-..or on a h tends vers 0

Flodelarab t'es toujours là ? ''désolée si je vous dérange''

[Flodelarab]

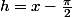
j'ai tenté en posant mais à la fin ça me donne un truc bizzare 1/h donc il faut avoir soit h tends vers 0+ ou 0-..or on a h tends vers 0

Flodelarab t'es toujours là ? ''désolée si je vous dérange''

Oui je suis la.
Je ne trouve pas que h change le probleme.
J'ai essayer de me passer des formules de trigo mais va falloir bidouiller sec.

[Flodelarab]

par contre, si on pose:
k=pi-x

alors on trouve que la limite est égale a son inverse.

Donc la limite ne peut etre que 1 ou -1

Et comme c négatif au voisinage pi/2 alors c -1

sur ce,

[sue]

je trouve un autre truc..

si on pose t=cosx alors x=Arccost..qd x tends vers pi/2 t tends vers 0

(j'ai multiplié le dénominateur et le numérateur par la quantité conjuguée)

j'espère que c juste .

merci Flodelarab c trés gentil .

bonne nuit.