* Question intéressante *

par **Dinozzo13** » 06 Nov 2009, 02:50

Bonjour, aujourd'hui, j'ai trouvé une question intéressante à laquelle je ne parviens pas à répondre, quelqu'un pourrait-il m'indiquer la démarche à suivre, merci d'avance. On me demande si la somme de deux suites non bornées peut-être une suite bornée.
Perso je pense que non, mais il n'y a pas de place pour l'approximation dans les maths et surtout dans ce genre de questions ^^.

par **romscau** » 06 Nov 2009, 09:02

tu considére la suite (un) tel que pour tout n Un = (-1) ^(2n)
et la suite (Vn) tel que pour tout n Vn = (-1) ^ (2n +1)

et la suite (Wn) défini pour tout n par Wn = Un + Vn est bornée ....

donc on peut trouver deux suites non bornée dont la somme est bornée

bonne journée

par **Dinozzo13** » 06 Nov 2009, 18:46

Angélique_64 a écrit:Si n'est pas bornée, tu poses

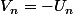
n'est pas bornée également.

Que peut on dire de ?

Je ne comprends ce que tu essaies de me faire démontrer :triste:

par **Nightmare** » 06 Nov 2009, 18:52

Ce que veut dire Angélique_64 c'est que si l'on prend U une suite non bornée, U-U est une suite bornée (puisque nulle) et est bien la somme de deux suites bornées ! (Car si U est bornée il en va de même pour -U évidemment)

par **Dinozzo13** » 06 Nov 2009, 18:53

ouh lala, je vais devoir réfléchir encore parce que là, ça ne me paraît pas hyper évident :triste: :cry:

par **Nightmare** » 06 Nov 2009, 18:55

Qu'est-ce que tu ne comprends pas?

On veut montrer qu'une somme de deux suites non bornée peut être bornée. Pour le montrer il suffit de trouver un exemple et moi je t'en donne un, si on prend U une suite quelconque non bornée. Alors la somme de U et -U (qui vaut 0) est une suite bornée. On a bien une somme de deux suites non bornées qui est bornée !

par **Dinozzo13** » 06 Nov 2009, 18:58

ah ! tu veux dire que la suite, admettons

, définie par

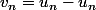
est bornée ? mais sur quoi l'est-elle ?

par **Nightmare** » 07 Nov 2009, 10:41

Ton incompréhension me laisse perplexe. Qu'est-ce qu'une suite bornée pour toi?

par **Dinozzo13** » 08 Nov 2009, 03:39

Selon moi une suite

est dite bornée si et seulement si, pour tout

, il existe un majorant

et un minorant

tels que

.

par **Nightmare** » 08 Nov 2009, 11:38

Donc il est clair que la suite U-U=0 (quelle que soit la suite U) est bornée non?

par **romscau** » 08 Nov 2009, 17:29

donc la suite Un = 0 est bordée
M =N =0 dans ta definition

*** Question intéressante ***