Question complexe
20 messages
- Page 1 sur 1
Re: question complexe
Et ouis,... peut-être... songer à regarder ton cours pour y trouver la définition de l'expression " forme trigonométrique"...silverseyf a écrit:Et puis ?
Je vais te donner une super astuce : quand dans une phrase (en Math., en Français, Anglais, etc...) y'a un mot dont tu ne connais pas le sens, ben pour comprendre le sens de la phrase, le premier truc à faire, c'est de chercher la définition du mot en question.
Pas con, non ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: question complexe
ici , |z|=√2 , d'ou cos(-x)=sin(-x)=√2/2 alors -x= pi/4 parsuite x=-pi/4 , c est juste ?
Re: question complexe
Comment fait tu, partant de z=cos(x)-i sin(x) pour trouver que |z|=√2 ? (c'est faux)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: question complexe
(I) :
(II) :
(III) :
Par contre je vois pas le rapport avec la question posée, à savoir :
Mimosa a écrit:Tu peux remarquer que
(II) :
silverseyf a écrit:z=cos(x)-isin(x)=cos(-x)+isin(-x)
(III) :
Réponse : oui, Mimosa "a juste".silverseyf a écrit:c est juste ou non !!?
Par contre je vois pas le rapport avec la question posée, à savoir :
Ben314 a écrit:Comment fait tu, partant de z=cos(x)-i sin(x) pour trouver que |z|=√2 ? (c'est faux)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: question complexe
soit z=a(cosx+isinx)
x appartient a ]0,pi[ , ecrire sous forme trigonometrique:
z1=cosx-isinx
J n arrive pas a comprendre comment je dois faire
x appartient a ]0,pi[ , ecrire sous forme trigonometrique:
z1=cosx-isinx
J n arrive pas a comprendre comment je dois faire
Re: question complexe
Ben déjà, il faudrait comprendre qu'un nombre complexe, ça s'écrit :
un_nombre_réel + i fois un_nombre_réel
et que le complexe qui s'écrit
z = cos(x) - i sin(x)
ben les deux nombres réels qui apparaissent dedans c'est pas 1 et 1 vu qu'on a pas du tout z = 1 + i 1.
1.
Bref, le module de z, c'est pas mais
mais 
un_nombre_réel + i fois un_nombre_réel
et que le complexe qui s'écrit
z = cos(x) - i sin(x)
ben les deux nombres réels qui apparaissent dedans c'est pas 1 et 1 vu qu'on a pas du tout z = 1 + i
Bref, le module de z, c'est pas
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: question complexe
Pff, le thread est un peu parti de travers
oui, comme déjà dit ⎷(cos²(-x)+sin²(-x)) = 1
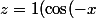+i\sin(-x)))
(qu'on pourra ensuite noter z=1 exp(-ix))
x est dans [0;pi[ et donc -x dans ]-pi;0]
[ EDIT] : cross post, et notation corrigée
oui, comme déjà dit ⎷(cos²(-x)+sin²(-x)) = 1
(qu'on pourra ensuite noter z=1 exp(-ix))
x est dans [0;pi[ et donc -x dans ]-pi;0]
[ EDIT] : cross post, et notation corrigée
Modifié en dernier par pascal16 le 10 Avr 2018, 10:26, modifié 2 fois.
Re: question complexe
Salut Pascal, il me semble qu'on lui demande la forme trigonométrique et non exponentielle du nombre complexe (meme si c'est juste une différence de notation ^^)
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
