Quelque révisions sur le barycentre et le produit scalaire

[Dinozzo13]

Bonjour, aujourd'hui, je révise le barycentre et le produit scalaire, j'aurai besoin de savoir, si ce que j'ai fait convient.
I:1°) Je cherche à déterminer, puis à construire, l'ensemble des points du plan tels que : , avec un triangle quelconque.
Soit le barycentre de ,,, donc d'après la propriété fondamentale, pour tout point du plan : .
équivaut à , .
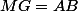
Donc l'ensemble des points du plan est le cercle de centre et de rayon .
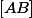
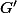
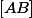
Pour construire , je nomme l'isobarycentre de et , c'est donc le milieu de . est le barycentre de ,,, donc d'après la propriété d'associativité, est aussi le barycentre de ,, donc par définition : équivaut à .
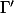
2°) Je cherche à déterminer, puis à construire, l'ensemble des points du plan tels que : .
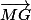
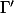
Or dans 1°), on a nommé G le barycentre de ,, et on a vu que : , donc, pour tout point M : équivaut à donc et sont orthogonaux. L'ensemble des points du plan est la droite perpendiculaire à passant par .

Ai-je bon ?

[benekire2]

Pour la première c'est bon.

[benekire2]

La deuxième aussi.

[Dinozzo13]

Je révise un peu comme ça le produit scalaire car je l'ai abordé à la fin de l'année de 1re S, donc j'essaie de voir ce qu'il me reste de l'an dernier ^^.
J'en ai fait un autre ^^.
III: On considère dans le plan deux points et tels que .
1°) Soit l'ensemble des points du plan tels que , déterminer .

Ici, l'idée est, je crois, d'introduire le point milieu de . Il vient ensuite, pour tout point :


Or est le milieu de donc et donc . Par conséquent :


Or donc
Et par conséquent, l'ensemble des points du plan est le cercle de centre et de rayon .

2°) Soit l'ensemble des points du plan tels que , déterminer .
De même, j'ultilise le point I milieu de [AB], pour tout M :


Comme I est le milieu de [AB], donc :

mais je doute là de ce que je trouve, je n'ai donc pas cherché à pour suivre l'exo.