Quelqu'un s'y connaitrait-il en trigo.? :D

[match0u]

J'aurais quelques petites questions, alors j'attends que les génies se manifestent :)

[Anonyme]

On est pas des génies ici juste des personnes qui sont intéressés par les maths. Pose tes questions et on te répondra . :++:

[Anonyme]

Bah quel niveau ?

[match0u]

alors voila voila, j'ai vraiment du mal avec les équations trigo, et deux trois autres choses.. Enfait quand je vois des sinus ou des cosinus ca me fait déja peur :p
1) Résoudre sin^4x + cos^4x = 3/4
2) [log (en base 2) de 2^(x+1) - 15 ] + x = 3
3) Intégrale de 1.dx / 5sinx + 4cosx + 5

Des idées du coté des interressés par les maths? :p

[Ericovitchi]

Pour la 1) l'astuce c'est d'abord de démontrer que sin^4x + cos^4x = 3/4 c'est pareil que résoudre cos(4 x) = 0

Pour la 2) le log en base 2 de 2^a c'est a donc l'équation devient toute simple

Pour l'intégrale, le plus simple est de se ramener à une fraction en posant t=tan(x/2)
le sin vaut 2t/1+t² le cos vaut (1-t²)/(1+t²), etc...
A la fin tu devrais trouver 1/4 (log(sin(x/2)+cos(x/2))-log(sin(x/2)+9 cos(x/2)))+constante

[match0u]

Je vais méditer à cela aussi :D Mais pour la 2ème question
2) [log (en base 2) de 2^(x+1) - 15 ] + x = 3
je comprends bien que log2 de 2^(x+1) devient simplement x+1, mais après il me reste encore le log2 de -15, et ca je ne vois pas quoi en faire :s

[Ericovitchi]

le -15 est dans le log aussi ?
donc c'est ton expression ?

[match0u]

Oui voila c'et ca, le -15 est dans le log aussi :)

[Ericovitchi]

Dans ce cas, il faut passer le x de l'autre coté puis prendre l'exponentielle 2^ des deux cotés, ca et donne
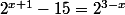
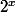
Tu ramènes les 2^ du même coté et tu passes le 15 de l'autre, tu poses X= et tu te ramènes à une équation du second degré

[match0u]

Un vrai génie, waouw :) Merci merci

[match0u]

Et en posant cela, ca donne bien 15= x - x^2

[Ericovitchi]

heu non : 2X²-15X-8=0 (d'où X=8 et x=3)

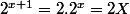
(car et )

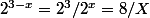
[match0u]

Lim( x -> 0) x.ln(1+x)-x^2 / (e^x) - (e^-x) - (2x)
Est ce que cela vous parle ? A moi non :D

[Ericovitchi]

Mets bien tes parenthèses. Je suppose que c'est :
(x.ln(1+x)-x^2 )/ ( (e^x) - (e^-x) - (2x) ) ?

Il faut faire des développements limités des fonctions et simplifier.
(si tu ne trompes pas, tu devrais trouver -3/2 comme limite)

[match0u]

J'arrive à -2/2, car état donné que la lim vaut 0/0, j'utilise la formule de l'Hospital, ce qui me donne 0/0 de nouveau, donc encore une fois l'Hospital, de nouveau 0/0, je recommence une dernière fois et je finis par obtenir -2/2..

[Ericovitchi]

ben non -1 c'est pas -3/2, tu as une erreur quelque part.

[match0u]

Ah oui je l'ai retrouvée :)

[benekire2]

ben non -1 c'est pas -3/2, tu as une erreur quelque part.

C'est bizarre moi aussi j'ai cru lire -3/2 , pourtant il a écrit -2/2 qui vaut bien -1 .... :id: