Qcm complexes

par **oliv9** » 28 Nov 2010, 18:47

rebonsoir j'ai encore un problème avec un qcm:

Soit n un entier naturel ,Le nombre (1+i racine (3))puissance n est réel si, et seulement si, n s'écrit sous la forme :
a)3k+1
b)3k+2
c)3k
d)6k

il faudrait que je trouve le module et argument de (1+i racine (3)) ou pas ? si oui que dois je faire aprés ?

par **Nightmare** » 28 Nov 2010, 18:48

Salut,

calculer l'argument est une bonne idée, pourquoi? Que sait-on de l'argument d'un réel?

par **oliv9** » 28 Nov 2010, 18:53

Tout réel positif a un argument égal à 0.
Tout réel négatif a un argument égal à pi

par **oliv9** » 28 Nov 2010, 19:04

j'ai trouvé un module de 2 et argument de pi /3

je dois l'écrire sous cette forme ou pas :arg z = pi/3 + 2kpi

si oui je ne vois pas de correspondance avec les resultats du qcm merci ?

par **Nightmare** » 28 Nov 2010, 19:15

Tu dis donc que ni le module, ni l'argument ne dépendent de n ? Je rappelle qu'on travaille avec

et non juste avec

.

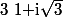
Il s'agit donc de calculer l'argument de (1+i rac(3))^n selon la valeur de n, puis déterminer les n pour lesquels l'argument vaut 0 ou pi !

par **oliv9** » 28 Nov 2010, 19:23

donc je devrai utilisé la formule de moivre non ?
(cos pi/3+isin pi/3)²

avec 3k=n

cos(3k x pi/3)+i sin(3k x pi /3)

= cos(kpi)+i sin(kpi)

c'est sa ?

par **Nightmare** » 28 Nov 2010, 19:27

Pas besoin de la formule de moivre, on sait plus simplement que

!

par **oliv9** » 28 Nov 2010, 19:34

donc quand j'ai trouvé mon argument qui est de (pi/3)^n j'ai juste a le multiplié par 3k pour trouver: kpi
donc la réponse est bien 3k ?

par **Nightmare** » 28 Nov 2010, 19:38

Non, l'argument n'est pas

mais

! Et on veut que ce soit égal soit à 0, soit à pi modulo 2pi (ou autrement dit, à 0 modulo pi), il faut donc bien que n soit de la forme 3k.

par **oliv9** » 28 Nov 2010, 20:12

je vien de me lancer sur un autre qcm mais pareil je ne vois jamais bien le sens de la question:

soit équation (E) :z = 6-z/3-z une solution de (E) est:

a)-2-rac(2) i
b) 2+ rac(2)i
c)1-i
d)-1-i

j'ai comencé a faire :(6-z)(3+z)/(3-z)(3+z)

je trouve: 18+3z-z²/6-z²

aprés je ne sais pas quoi faire j'allais me lancer dans un delta=b²-4ac mais nous avons pas vu le chapitre en classe donc sa doit etre pas sa, je crois que je me complique la vie mdr merci

par **Sylviel** » 28 Nov 2010, 20:29

parenthèses !

Pour voir si c'est une solution il suffit de remplacer z par la valeur proposée et de voir si oui ou non l'équation est vérifiée...

par **oliv9** » 28 Nov 2010, 21:04

je n'est pas trés bien compris en fait je doit z par quoi ?

par **Sylviel** » 28 Nov 2010, 21:13

soit équation (E) :z = 6-z/3-z une solution de (E) est:
a)-2-rac(2) i
b) 2+ rac(2)i
c)1-i
d)-1-i

Et bien par exemple si tu veux savoir si 1-i est solution il suffit de calculer
6-z/3-z (quoique cela signifie) pour z = 1-i et de regarder si cela vaut bien ... 1-i !

par **oliv9** » 28 Nov 2010, 21:30

j'ai remplacer z par la reponce b et j'ai trouver 2-rac(2)i c'est normal?

Qcm complexes

qcm complexes

Qui est en ligne