Python et équation

[Alessandra]

Bonjour, pouvez-vous m'aider à cet exercice s'il vous plaît ?

On considère l'équation (E): e^x =x+2
1) Démontrer que l'équation (E) admet exactement deux solutions dans R et que ces deux solutions sont de signes opposés. (On n'encadrera pas ces solutions)

2) Recopier et compléter la fonction encadrement en Python afin que celle-ci renvoie un encadrement d'amplitude 10^-4 de la solution positive de (E) lorsqu'on écrit encadrement(4) dans la console. Donner alors cet encadrement.

Le programme:

from math import exp

def encadrement (p):
x=0
y= -1
while y < ... :
x = ...
y = ...
return ... , ...

Merci d'avance

[Roc]

Bonjour,
Pour la question 1, tu peux déjà tracer une fonction "exp(x)" et une autre d'expression "x + 2" comme ci-dessous:



Tu as déjà un aperçu sur la position des solutions x.
Sinon tu peux tout simplement considérer la fonction et faire sa dérivée pour avoir sa variation dans R. Les solutions seront trouvées lorsque car d'où :
Tu trouveras donc que la fonction f(x) est décroissante de +infini à - 1 pour x compris entre [-infini,0] et croissante de -1 à + infini pour x entre [0,+infini].

Ce qui veut dire que ta fonction s'annule pour un x négatif compris entre [-infini,0] (car de + infini à -1 : on passe forcément par 0 car fonction continue) et pour un x positif compris entre [0,+infini]. .

Maintenant pour le programme python :
Retient bien que x correspond aux solutions (axe des abscisses) qu'on cherche et y correspond à l'image (axe des ordonnées), donc:

il faut trouver les solutions x pour lesquelles la fonction s'annule...
Donc pour x = 0 --> y = exp(0) - 0 - 2 = 1 - 2 = -1
Voilà pourquoi au début du programme on définit x = 0 et y = -1
Donc While (tant que ....) y n'est pas nul (donc y < ...) on entre dans la boucle...

Dans la boucle on va ajouter à chaque fois à x une valeur de pour avoir par exemple une amplitude de 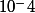si p = 4 et pour calculer y tu as l'expression de f(x)....

[Alessandra]

Bonjour, merci beaucoup pour votre aide. Mais je n'ai toujours pas compris l'algorithme.

Merci

[Roc]

Tu as compris ce que tu peux faire à la question 1 ?
Pour le programme python, on considère une fonction et on cherche les solutions x pour lesquelles f(x) = 0.
Pour commencer, l'énoncé t'aide un peu en définissant sur python une fonction encadrement(p) de paramètre p.
Ensuite, la première valeur de y ou f(x) est définie pour la première valeur de x = 0, ce qui donne y = f(0) = -1.

Comme dit, on cherche les solutions x pour lesquelles y s'annule : donc on fait appel à la boucle while (qui veut dire tant que) qui va nous permettre de calculer y pour chaque x jusqu'à ce que y soit nul...

Il faut mettre une condition après le while qui va faire intervenir y : pour la trouver, il faut savoir que tant que cette condition est vraie, je rentre dans la boucle :

par exemple :
while t > 2:
t = t + 1

Ici, tant que t > 2 j'ajoute 1 à t....

Dans notre cas tant que y est inférieur à 0 alors je rentre dans la boucle while :
Maintenant dans la boucle, il faut incrémenter x (lui ajouter une valeur à chaque tour de boucle d'une valeur 10^(-p)) et calculer y en lui donnant son expression (la même que f(x)).
En sortie de boucle, je suis censé avoir trouvé le x positif pour lequel y = 0.....

[Alessandra]

Pour la question 1 j'ai compris qu'il fallait dérivé la fonction f(x)=exp(x)-x-2 ce qui donne f'(x)= exp(x)-1
On doit donc faire un tableau de variation : le signe de f'(x) permet de déterminer les variations de f(x).

Pour la question 2 j'ai donc fait cela:

From math import exp

def encadrement (p):
x=0
y=-1
while y<0:
x=x+10^(-p)
y= exp(x)-x-2
return x,y

Est-ce cela ?

[Roc]

Ça me parait juste, n’oublie pas d’appeler la fonction si tu compte écrire le programme sur ordinateur.

[hdci]

Juste un détail : la fonction doit retourner un encadrement, donc un x1 et un x2.
Or ici elle retourne un x et son image.

Comme la boucle s'arête dès que l'image de x est positive, cela signifie que x-10^(-p) a une image négative et cela donne l'encadrement.

[Alessandra]

Je n'arrive pas à trouver l'encadrement lorsque je rentre le programme python même quand je fais des changements.

[hdci]

Attention, en python la puissance s'écrit **

C'est donc x = x+10**(-p) qu'il faut écrire.

Sinon à part cela c'est correct (je viens de tester), avec juste à la fin : supposons que le pas soit 10**(-3), alors on part de 0 et on ajoute successivement 0.001 jusqu'à ce que la fonction rende un résultat positif.
Donc quand vous quittez la boucle, la variable x contient la première valeur telle que l'image est positive.
Cela veut donc dire que la valeur juste avant, c'est-à-dire avant qu'on ajoute 10**(-3), avait une valeur négative.

Donc dans votr return, x contient un nombre dont l'image est positive, et x - 10**(-3) contient "le nombre d'avant", dont l'image est négative. Le véritable antécédent de zéro est donc compris entre x-10**(-3) et x ce qui fait bien un encadrement de 10 puissance -3.

Remplacez 3 par p dans ce que je viens de dire et vous avez la réponse.

[Alessandra]

J'ai écrit cela sur python:
from math import exp

def encadrement (p):
x=0
y=-1
while y < 0 :
x = x+10**(-3)
y = exp(x)-x-2
return x,y
print(encadrement(3))

et cela me renvoie : (1.1469999999999845, 0.0017325286275431395)
Cela me paraît étrange.

[hdci]

Non c'est normal.
C'est parce que l'ordinateur n'a pas une représentation décimale, mais une représentation binaire.

En décimal, 1/10 est un nombre qui s'écrit avec un nombre fini de décimales : 0,1.

Mais en binaire (les seuls chiffres étant 0 et 1), 1/10 est un nombre qui s'écrit avec une infinité de décimales (exactement comme 1/3 en décimal : 1/3=0,333.... mais les 3 ne s'arrêtent jamais).
Le truc c'est que l'ordinateur ne peut pas mémoriser toutes les décimales. Donc à un moment il "coupe".

Ce qui fait un "arrondi" et l'erreur d'arrondi se propage au fur et à mesure des calculs.
Heureusement, l'arrondi se fait à une décimale très lointaine, ce qui fait que si on ne regarde que les 3 ou 4 premières décimales, on obtient un résultat plus parlant : ainsi, 1.1469999999999845 devrait en fait se lire 1.147 en arrondissant à la 3ème décimale.

Quant à votre 0.0017325286275431395, relisez bien ce que j'ai écrit dans mes précédents messages : vous ne renvoyez pas un encadrement, mais vous renvoyez la première valeur de x dont l'image dépasse 0, virgule, l'image de cet x.
Or il faut renvoyer un encadrement, c'est-à-dire a dernière valeur de x qui a une image négative, suivi de la première valeur de x qui a une image positive.

[Alessandra]

Bonjour,
L'encadrement est donc:
1,1461<x<1,1462

Merci