Putnam 1993
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 19 Nov 2013, 20:43
par t.itou29 » 19 Nov 2013, 20:43
Bonsoir,
Je bloque sur ce problème:
La droite horizontale d'équation
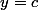
(1) intercepte la courbe d'équation
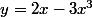
(2). Trouver c tel que les aires des surfaces en noires soient égales (voir schéma).
https://drive.google.com/file/d/0B2uj8lrnLJwSYzB2VEV6TFRpSjQ/edit?usp=sharingA première vue c'est accessible en ts. Les deux aires sont égales si l'aire sous la courbe (2) est égale à l'aire de la surface en rouge sur le dessin. Je pensais la décomposer en un rectangle et une partie de la courbe (2) mais je ne vois pas comment déterminer simplement l'abscisse du point d'intersection, c'est à dire la solution de
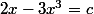
.
Peut-être que ma technique ne mène à rien mais je ne vois pas quoi faire d'autre ?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 19 Nov 2013, 20:46
par Sourire_banane » 19 Nov 2013, 20:46
t.itou29 a écrit:Bonsoir,
Je bloque sur ce problème:
La droite horizontale d'équation
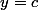
(1) intercepte la courbe d'équation
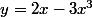
(2). Trouver c tel que les aires des surfaces en noires soient égales (voir schéma).
https://drive.google.com/file/d/0B2uj8lrnLJwSYzB2VEV6TFRpSjQ/edit?usp=sharingA première vue c'est accessible en ts. Les deux aires sont égales si l'aire sous la courbe (2) est égale à l'aire de la surface en rouge sur le dessin. Je pensais la décomposer en un rectangle et une partie de la courbe (2) mais je ne vois pas comment déterminer simplement l'abscisse du point d'intersection, c'est à dire la solution de
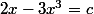
.
Peut-être que ma technique ne mène à rien mais je ne vois pas quoi faire d'autre ?
Salut,
Exprime en fonction de c les abscisses d'intersection de D1:y=c avec C1:y=f(x).
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 19 Nov 2013, 21:10
par t.itou29 » 19 Nov 2013, 21:10
Sourire_banane a écrit:Salut,
Exprime en fonction de c les abscisses d'intersection de D1:y=c avec C1:y=f(x).
J'ai essayé mais avec le 3ème degré je tombe (enfin wolfram alpha) sur une expression horrible. C'est pour ça je me demande si ma méthode mène a quelque chose
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 19 Nov 2013, 22:04
par Sourire_banane » 19 Nov 2013, 22:04
Ok,
Plutôt, nomme les deux abscisses où f(x)-c change de signe, pour la valeur de c voulue.
Prends une des abscisses. Appelons-la a.
Alors clairement on doit avoir l'aire de gauche = aire de droite
Donc aire de gauche - aire de droite = 0
Cela revient à soustraire du rectangle d'aire ac la portion d'aire sous la courbe jusqu'à x=a.
Donc
dx=a(2a-3a^3)-\int_0^a (2x-3x^3)dx=0)
avec c=f(a)
Résous cette équation.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 20 Nov 2013, 09:29
par chan79 » 20 Nov 2013, 09:29
Salut
Soient a et b les deux valeurs telles que f(a)=f(b)=c avec a<b
on sait que 2a-3a³=2b-3b³=c
il faut résoudre:
dx=\bigint_{a}^{b}(2x-x^3)dx - c(b-a))
Ca se simplifie pas mal et tu dois trouver c=4/9
Le mieux est de chercher d'abord la valeur de b
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 20 Nov 2013, 12:19
par t.itou29 » 20 Nov 2013, 12:19
chan79 a écrit:Salut
Soient a et b les deux valeurs telles f(a)=f(b)=c avec a<b
on sait que 2a-3a³=2b-3b³=c
il faut résoudre:
dx=\bigint_{a}^{b}(2x-x^3)dx - c(b-a))
Ca se simplifie pas mal et tu dois trouver c=4/9
Le mieux est de chercher d'abord la valeur de b
Ok merci, je vais essayer, je renvoie un message quand j'ai réussi
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 20 Nov 2013, 17:06
par t.itou29 » 20 Nov 2013, 17:06
Je suis arrivé à
dx)
Ce qui mène à :

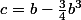
comme
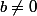
-b+\frac{9}{4}b^3)

On trouve
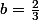
et donc
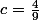
Merci beaucoup !

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 20 Nov 2013, 18:08
par chan79 » 20 Nov 2013, 18:08
t.itou29 a écrit:Je suis arrivé à
dx)
Ce qui mène à :

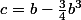
comme
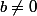
-b+\frac{9}{4}b^3)

On trouve
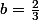
et donc
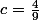
Merci beaucoup !
On est d'accord
Tu peux t'amuser à calculer l'aire de chacune de ces zones (indiquée ci-dessous)

Uploaded with
ImageShack.us
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 24 Nov 2013, 11:35
par t.itou29 » 24 Nov 2013, 11:35
chan79 a écrit:On est d'accord
Tu peux t'amuser à calculer l'aire de chacune de ces zones (indiquée ci-dessous)

Uploaded with
ImageShack.us
Désolé de ma réponse tardive, il y a juste à déterminer a et calculer l'intégrale ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités

